Why you should be using Differential Evolution for your optimization problems.

What is this sorcery?

What is Differential Evolution (DE) and how does it work?

In facy words, it “ is a method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality”. It does so by, optimizing “a problem by maintaining a population of candidate solutions and creating new candidate solutions by combining existing ones according to its simple formulae, and then keeping whichever candidate solution has the best score or fitness on the optimization problem at hand”.

Simply put, Differential Evolution will go over each of the solutions. If it matches criterion (meets minimum score for instance), it will be added to the list of candidate solutions. New solutions might be found by doing simple math operations on candidate solutions. When iterations are finished, we take the solution with the highest score (or whatever criterion we want).

To build DE based optimizer we can follow the following steps.

This provides a very high level view of the code. This is because most of these steps are very problem dependent. Use the image as reference for the steps required for implementing DE. If you would like to build a more complex function based optimizer the instructions below are perfect

These slides are great reference for beginners. They covers the basics very well. Made by a Professor at IIT (India’s premier Tech college), they demystify the steps in an actionable way.

Alternatively, I’ve made a video, going over DE and why it’s super-duper cool. Check it out here. And always remember to like, subscribe and share any feedback you might have :) :

Selling Points of DE

Now that we understand the basics behind DE, it’s time to drill down into the pros and cons of this method. This will help you understand when DE might be a better-optimizing protocol to follow.

Range

Here a,b,c show 3 ways a function can not be differentiable

The biggest benefit of DE comes from its flexibility. Since it doesn’t evaluate the gradient at a point, IT DOESN’T NEED DIFFERENTIALABLE FUNCTIONS. This is not to be overlooked. For a function to be differentiable, it needs to have a derivative at every point over the domain. This requires a regular function, without bends, gaps, etc. DE doesn’t care about the nature of these functions. They can work well on continuous and discrete functions. DEs can thus be (and have been)used to optimize for many real-world problems with fantastic results. I will be elaborating on this in the next section.

Performance

Keep in mind that Deep Neural Networks take millions of times more resources.

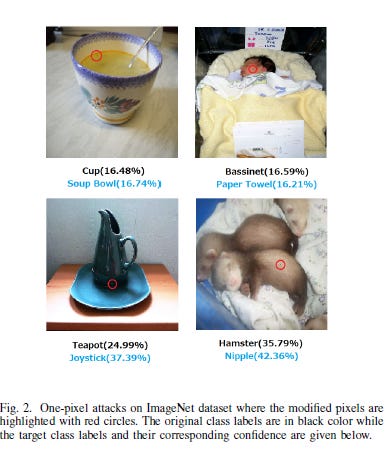
The range means nothing if not backed by solid performances. And DEs can even outperform more expensive gradient-based methods. Take the fantastic One Pixel Attack paper(article coming soon). It is able to fool Deep Neural Networks trained to classify images by changing only one pixel in the image (look left). The team uses DE to optimize since Differential Evolution “Can attack more types of DNNs (e.g. networks that are not differentiable or when the gradient calculation is difficult).” And the results speak for themselves. “On Kaggle CIFAR-10 dataset, being able to launch non-targeted attacks by only modifying one pixel on three common deep neural network structures with 68:71%, 71:66% and 63:53% success rates.” Similarly “Differential Evolution with Novel Mutation and Adaptive Crossover Strategies for Solving Large Scale Global Optimization Problems” highlights the use of Differential Evolutional to optimize complex, high-dimensional problems in real-world situations. The range allows it to be used on all types of problems. And always remember: it is computationally inexpensive.

Simplicity

Differential Evolution is not too concerned with the kind of input due to its simplicity. The simplicity adds another benefit. It can be improved easily. Papers have shown a vast array of techniques that can be bootstrapped into Differential Evolution to create a DE optimizer that excels at specific problems. I would searching Google for examples related to your specific domain to see possible techniques. The one I found coolest was: “Differential Evolution with Simulated Annealing.”

Semi-Black Box when dealing with DNNs

DE is not a black-box algorithm. The functioning and process are very transparent. This makes it very good for tracing steps, and fine-tuning. It requires black-box feedback(probability labels)when dealing with Deep Neural Networks. However, this is the only case with some opacity.

Final Thoughts

DEs are very powerful. Their popularity can be boiled down to a simple slogan, “Low Cost, High Performance for a larger variety of problems”. Due to their low cost, I would suggest adding DE to your analysis, even if you know that your function is differentiable. Since DEs are based on another system they can complement your gradient-based optimization very nicely.

For Machine Learning a base in Software Engineering, Math, and Computer Science is crucial. It will help you conceptualize, build, and optimize your ML. My daily newsletter, Technology Made Simple covers topics in Algorithm Design, Math, Recent Events in Tech, Software Engineering, and much more to make you a better Machine Learning Engineer. I have a special discount for my readers.

Save the time, energy, and money you would burn by going through all those videos, courses, products, and ‘coaches’ and easily find all your needs met in one place.

I am currently running a 20% discount for a WHOLE YEAR, so make sure to check it out. Using this discount will drop the prices-

800 INR (10 USD) → 533 INR (8 USD) per Month

8000 INR (100 USD) → 6400INR (80 USD) per year

You can learn more about the newsletter here. If you’d like to talk to me about your project/company/organization, scroll below and use my contact links to reach out to me.

Reach out to me

Use the links below to check out my other content, learn more about tutoring, reach out to me about projects, or just to say hi.

If you like my writing, I would really appreciate an anonymous testimonial. You can drop it here.

To help me understand you fill out this survey (anonymous)

Check out my other articles on Medium. : https://rb.gy/zn1aiu

My YouTube: https://rb.gy/88iwdd

Reach out to me on LinkedIn. Let’s connect: https://rb.gy/m5ok2y

My Instagram: https://rb.gy/gmvuy9

My Twitter: https://twitter.com/Machine01776819