Can Natural Gradients replace Gradient Descent [Investigations]
Your introduction to the Natural Gradient and why they have the potential so amazing
Hey, it’s Devansh 👋👋
Some questions require a lot of nuance and research to answer (“Do LLMs understand Languages”, “How Do Batch Sizes Impact DL” etc.). In Investigations, I collate multiple research points to answer one over-arching question. The goal is to give you a great starting point for some of the most important questions in AI and Tech.
I put a lot of effort into creating work that is informative, useful, and independent from undue influence. If you’d like to support my writing, consider becoming a premium subscriber to my sister publication Tech Made Simple to support my crippling chocolate milk addiction. Use the button below for a lifetime 50% discount (5 USD/month, or 50 USD/year).
Executive Highlights
1.5 months ago Manny Ko- principal engineer at Apple and geometric deep learning + Computer Vision expert- decided to continue his assault on my self-confidence by introducing me to Natural Gradients. Natural Gradients seek to improve Gradient Descent by reducing the ‘destructive updates’ involved in the backprop process.
The implications of such an idea can’t be overlooked. If it works, such an algorithm allows for both wider (more data/modalities) and deeper (improving existing NNs) adoption of neural networks. As we discussed in our investigation on Complex Valued Neural Networks, there is a lot to be gained by giving Neural Networks a new dimension to process. Natural Gradients do this by considering additional information when computing the updates. The results are promising-
We conclude that the natural gradient can significantly improve performance in terms of wall-clock time. For ill-conditioned posteriors the benefit of the natural gradient method is especially pronounced, and we demonstrate a practical setting where ordinary gradients are unusable. We show how natural gradients can be computed efficiently and automatically in any parameterization, using automatic differentiation.
- “Natural Gradients in Practice: Non-Conjugate Variational Inference in Gaussian Process Models”
The power of Natural Gradients lies in two simple observations. Every new update overwrites prior training. Done over a long enough time frame, this leads to a loss of ‘insights’ that a model might have learned in the early iterations. Natural Gradients seek to minimize this by ensuring that the model updates don’t diverge drastically from the source. GD also doesn’t consider the curvature of the function. NGD fixes this, leading to faster convergence and a natural defense against getting stuck in the local minima.
Unfortunately, this additional computation has made it computationally infeasible to implement NGD at scale. This overhead was a death sentence, but we have recently seen some great research that gives us a way possibilities for expanding this beyond small networks and theoretical experiments.
In this paper, we develop an efficient sketch-based empirical natural gradient method (SENG) for large-scale deep learning problems…Extensive experiments on convolutional neural networks show the competitiveness of SENG compared with the state-of-the-art methods. On the task ResNet50 with ImageNet-1k, SENG achieves 75.9% Top-1 testing accuracy within 41 epochs. Experiments on the distributed large-batch training Resnet50 with ImageNet-1k show that the scaling efficiency is quite reasonable.
— “Sketch-Based Empirical Natural Gradient Methods for Deep Learning”
In the rest of this investigation, we will explore the idea of Natural Gradients in more detail. We will talk about the flaws of normal gradient descent, how NDs can solve them, and how we can tackle the scaling issues of NDs. Given how esoteric this is, I would strongly experimenting with the ideas discussed here. Your experiments could end up being key to pushing this sub-field further.
Before we proceed, I would like to also take a second to thank Ravindranath Nemani, Data Scientist at IBM India, for sharing some great writeups on this topic. The only reason I can self-study and write about these very dense topics is thanks to experts like him using their years of experience to guide me along interesting/relevant paths.
Where Gradient Descent Falls Short
Let’s take a second to see how the gradients are calculated in normal GD.
This algorithm makes a very subtle but massive assumption. Take a second to think about what it is, moving on.
If you’re feeling particularly brave, take a guess what I’m about to say before reading on. If you get it right, I’ll buy you a cookie whenever we meet.
The problems with SGD can be summed up by a simple sentence- SGD is like a brainwashing communist. Let’s unpack that.
Firstly, take a look at the learning rate. Our gradient is a vector, which we are multiplying by the scalar LR. By doing so, we scale up the update along each parameter axis by the same fixed amount in terms of Euclidean parameter distance.
Remember parameters have very different data distributions. They will also have impact your training differently. A fixed scaling doesn’t really account for this. In this forced equality, SGD is very much like a hippie or (even worse) a COMMIE!! And do we really want someone like that making decisions about our AI? I think not. We need a way to account for the differences in parameters instead of equating things based on a simplistic distance metric.

But that’s not all folks. Not only does SGD mooch off from our hard-working parameters, but it also experiences something called destructive interference. As mentioned earlier, newer updates have the potential to overwrite earlier data, in a sense “destroying prior learning” (this is something that Dr. Lambos had mentioned in his guest post, a long time back). Let the model spend long enough with the SGD, and it will eventually forget its homegrown values.
To reiterate, SGD is a brainwashing commie. So how can we address this issue? Let’s take a look at what we would need to solve the problems-
Solving Destructive Interference- Ideally, we would want our training to move along a gradient while keeping our prior learning intact. This way, our traditional values will live on while our baby model interacts with new data.
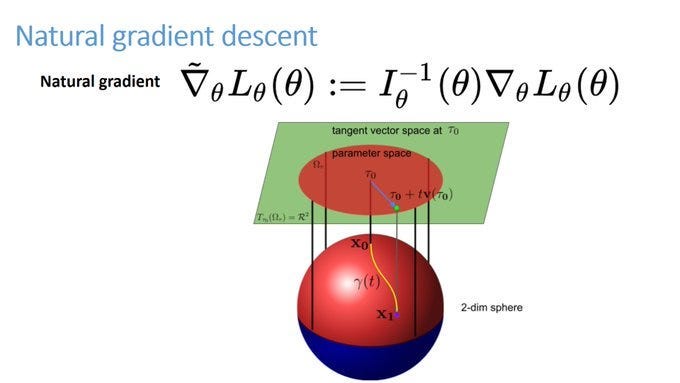
Accounting for Differences- Presently, the optimization in gradient descent is dependent to the Euclidean geometry of the parameter space. If our objective is to minimize the loss function, then it is natural to take steps in the space of all possible likelihood. Since the likelihood function itself is a probability distribution, we call this space distribution space. Thus it makes sense to take the steepest descent direction in this distribution space instead of parameter space. The utilization of a distribution space also would make our computations invariant to reparameterization.
Natural Gradient is great because it handles both of these. Let’s talk about how.

Understanding the Natural Gradient Descent
I spent some time on the problems of SGD because the formulation for NGD can be a bit strange. I know my first time seeing it without more context left me with a lot of questions. Here is the formulation for the natural gradient. In a nutshell, we multiply the gradient of the loss with the inverse of the Fisher Information Matrix.

Aside from style points, what does this accomplish? The first part is pretty simple, so let’s hone in on the Fisher Matrix. For complex, mathy reasons- KL Divergence is not a valid metric for distances (since the divergence is not symmetric). But are we really going to let mathematicians tell us what to do? Giga chads like us don’t need to follow the rules. Turns out that if you make the neighborhoods small enough, KL Divergence does behave like a metric. If we take the second derivative of KL Divergence (wrt to the parameters), we now understand how the KL Divergence fluctuates when we get jiggy with the parameters. High fluctuation bad. Low Fluctutation good.
So what does this have to do with the Fisher Information? Turns out, the Fisher Information approximates the second derivative of the divergence. The way I understand it, the Fisher information matrix is good for understanding how much information your data holds about the unknowns you’re trying to estimate. When it comes to the formulation, there are three decisions that we need to understand-
We square the log-likelihood to get the absolute value.
This derivative tells us how rapidly the log-likelihood changes as we tweak the parameters.
We compute the expected value to give us the average amount of information a set of data provides about the unknown parameters.
Hopefully, it starts to make sense why this is important in natural gradients. Fisher Information allows us to capture the curvature of the parameter space. If we see a lot of fluctuation in a particular parameter direction, it will have a higher value in the Fisher Information Matrix, and thus we will have a smaller update step in that direction.
This ends most of the math explanations for this piece. If you think I missed something, got anything wrong, or could have explained something better- please let me know. It’s always challenging to explain mathematical intuition in English. I’m also completely self-taught, so I no doubt have holes in my theoretical knowledge. Any critique or feedback will only help me create better work for the future.
The more observant amongst you might have noticed something- this is a second-order method. Second-order Methods like ADAM have become mainstream b/c of their ability to navigate the high noise from first-order methods better. So why didn’t this take off the way others did?
Simply put, calculating the FIM at every step is a wee-bit tedious. Sure this will lead to faster convergence since you are taking the optimal step, but the amount of overthinking your model has to do to the right decision makes the whole process pointless (bet you weren’t expecting that little life lesson). This has been the bane of Natural Gradients. Luckily, we are seeing some great options for approximating this by the utilization of various techniques.
Let’s end on a discussion of some of some good research papers that I found that show potential for scaling up natural gradients further. In the interest of not making this too long, I’ll keep this to a summary. If these ideas interest you, I can do a follow-up on the papers.
Scaling up Natural Gradients.
The core idea behind scaling up Natural Gradients is approximations. Wherever we can, we go for good enough.
Scalable and Practical Natural Gradient for Large-Scale Deep Learning
This is the best paper for engineering insights and scaling NGD. Here the authors use lots of little tricks to approximate numbers in computations.
We demonstrate convergence to a top-1 validation accuracy of 75.4% in 5.5 minutes using a mini-batch size of 32,768 with 1,024 GPUs, as well as an accuracy of 74.9% with an extremely large mini-batch size of 131,072 in 873 steps of SP-NGD.
To accomplish this scale, they make the following approximations to the FIM-
We further use KFAC to approximate the second order derivatives. This works both for convolutions and Fully-Connected Layers. This is combined with the utilization of Emperical Fisher and using stale stats. To reach distributed scales, this is also combine with some engineering tricks like mixed precision computing and utilizing symmetry.
Fast Convergence of Natural Gradient Descent for Overparameterized Neural Networks
This paper has the following contributions:
“We identify two conditions which guarantee efficient convergence from random initializations: (1) the Jacobian matrix (of network’s output for all training cases with respect to the parameters) has full row rank, and (2) the Jacobian matrix is stable for small perturbations around the initialization.”
“For two-layer ReLU neural networks, we prove that these two conditions do in fact hold throughout the training, under the assumptions of nondegenerate inputs and overparameterization.”
“We further extend our analysis to more general loss functions.”
“Lastly, we show that K-FAC, an approximate natural gradient descent method, also converges to global minima under the same assumptions, and we give a bound on the rate of this convergence.”
Beyond that, we also showed that the improved convergence rates don’t come at the expense of worse generalization (although we’re only testing with 2-layer ReLU networks here).
This paper is a lot of proofs. For our purposes, it is enough to look at the KFAC approximation. That is the most useful part for implementation/trial and error purposes.
Achieving High Accuracy with PINNs via Energy Natural Gradient Descent
I’m not entirely sure I understand Physics Informed Neural Networks (PINNs), but immediately what stood out to me was the conversation of orthognality (another idea I have to look into and discuss at length). And check the results-
We demonstrate experimentally that energy natural gradient descent yields highly accurate solutions with errors several orders of magnitude smaller than what is obtained when training PINNs with standard optimizers like gradient descent or Adam, even when those are allowed significantly more computation time.
Numbers wise, they are not overstating their claims-
A pretty interesting comparison on costs b/w ND and Adam was also made, that contextualizes the entire debate-
“With our current implementation and the network sizes we consider, one natural gradient update is only twice to three times as costly as one iteration of the Adam algorithm, compare also to Table 2. Training a PINN model with optimizers such as Adam easily requires 100 times the amount of iterations — without being able to produce highly accurate solutions — of what we found necessary for natural gradient training, rendering the proposed approach both faster and more accurate”
Finally, this shows good potential with more dimensions, addressing the problems of Natural Gradients. Although this is still only 5 dimensions, not the thousands in some Deep Learning Applications. That’s we’re going to need one of you madlads to nuke your AI Pipelines for science by trying this out. I look forward to hearing how it goes.

Honorable Mention- Efficient and convergent natural gradient based optimization algorithms for machine learning
The natural gradient can be computed fast for particular manifolds named Dually Flat Manifold or DFM. Don’t ask me what they are, this is still something I need to learn about. Turns out that the Multinomial Logistic Regression (MLR) problem, can be adapted and solved by taking a DFM as the model. This looks promising, but I need to go into this a lot more before making any conclusions.
Honorable Mention Part 2- Efficient Natural Gradient Descent Methods for Large-Scale PDE-Based Optimization Problems
Our technique represents the natural gradient direction as a solution to a standard least-squares problem. Hence, instead of calculating, storing, or inverting the information matrix directly, we apply efficient methods from numerical linear algebra. We treat both scenarios where the Jacobian, i.e., the derivative of the state variable with respect to the parameter, is either explicitly known or implicitly given through constraints. We can thus reliably compute several natural NGDs for a large-scale parameter space. In particular, we are able to compute Wasserstein NGD in thousands of dimensions, which was believed to be out of reach. Finally, our numerical results shed light on the qualitative differences between the standard gradient descent and various NGD methods based on different metric spaces in nonconvex optimization problems.
Do you have any thoughts about Natural Gradients? Let me know.
If you liked this article and wish to share it, please refer to the following guidelines.
That is it for this piece. I appreciate your time. As always, if you’re interested in working with me or checking out my other work, my links will be at the end of this email/post. And if you found value in this write-up, I would appreciate you sharing it with more people. It is word-of-mouth referrals like yours that help me grow.
Reach out to me
Use the links below to check out my other content, learn more about tutoring, reach out to me about projects, or just to say hi.
Small Snippets about Tech, AI and Machine Learning over here
AI Newsletter- https://artificialintelligencemadesimple.substack.com/
My grandma’s favorite Tech Newsletter- https://codinginterviewsmadesimple.substack.com/
Check out my other articles on Medium. : https://rb.gy/zn1aiu
My YouTube: https://rb.gy/88iwdd
Reach out to me on LinkedIn. Let’s connect: https://rb.gy/m5ok2y
My Instagram: https://rb.gy/gmvuy9
My Twitter: https://twitter.com/Machine01776819