How Google discovered the Swish Activation Function [Breakdown]

And how good is it?

Hey, it’s Devansh 👋👋

In my series Breakdowns, I go through complicated literature on Machine Learning to extract the most valuable insights. Expect concise, jargon-free, but still useful analysis aimed at helping you understand the intricacies of Cutting-Edge AI Research and the applications of Deep Learning at the highest level.

If you’d like to support my writing, consider becoming a premium subscriber to my sister publication Tech Made Simple to support my crippling chocolate milk addiction. Use the button below for a lifetime 50% discount (5 USD/month, or 50 USD/year).

---

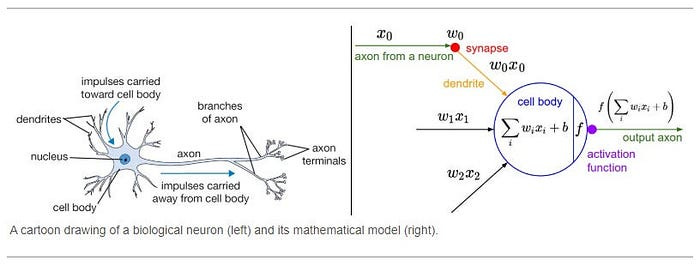
As you will know, research into Neural Networks has a lot more than just model architecture. There is tons of research into different data imputation policies, learning rates, and batch sizes (all of which I have covered prior) to maximize performance. One of the most important aspects of a neural network is its activation function. In Machine Learning, the activation function of a node defines the output of that node given an input or set of inputs. In a sense, your activation function defines how your neural network processes its inputs. making it one of the more important decisions when setting up your model architecture.

Image Source

In this article, we will be covering the Google Publication “Searching for Activation Functions”, where researchers discover and compare various activation functions (in an automated way). In this article we will be covering the following-

1. Why searching for activation functions is a big deal/

2. How Google Researchers automated the search for new activation functions (to me, this is the most important takeaway from this paper)

3. What this paper teaches us about Activation Functions.

4. A look into the Swish Activation Function.

5. Evaluating Swish on a few benchmarks.

I hope you’re excited for this one.

A quantitative look at the impact of Activation Functions

Before we proceed, some of you are without a doubt skeptical about the impact of activation functions. Peep the following quote from the paper:

On ImageNet, replacing ReLUs with Swish units improves top-1 classification accuracy by 0.9% on Mobile NASNet-A (Zoph et al., 2017) and 0.6% on Inception-ResNet-v2 (Szegedy et al., 2017). These accuracy gains are significant given that one year of architectural tuning and enlarging yielded 1.3% accuracy improvement going from Inception V3 (Szegedy et al., 2016) to Inception-ResNet-v2 (Szegedy et al., 2017).

In case you’re not convinced, reread that. Just replacing the activation function from ReLU (the standard these days) to Swish (we’ll cover it), improved performance almost as much as tuning and enlarging a giant model for 1 year. Research into various activation functions and how they interact with different kinds of inputs is worth it.

Now of course, once we start dealing with supermassive models, this stops being as important. Supergiant models act as quasi-universal approximators, so the only real way to improve them is to improve the data quality and variety (good data is the most important for all AI, but with giants, it especially overshadows everything else). However, in most cases, you’ll probably be using much smaller models for your tasks. In this case, it’s worthwhile to pay attention to these architectural nuances.

How to find the best activation functions

Now that we have established how important Machine Learning activation functions are, let’s talk about how the researchers found them. Traditionally, activation functions have been hand-crafted (to match certain criteria). However, this process can get expensive (and slow) very quickly. Instead, the researchers here used a combination of exhaustive search (for smaller search spaces)and an RNN-based controller (for larger search spaces). They ran their search over the following functions-

These small functions are combined to create our activation functions. The activation function is constructed by repeatedly composing the “core unit”, which is defined as b(u1(x1), u2(x2)). The core unit takes in two scalar inputs, passes each input independently through an unary function, and combines the two unary outputs with a binary function that outputs a scalar. Since we aim to find scalar activation functions that transform a single scalar input into a single scalar output, the inputs of the unary functions are restricted to the layer preactivation x, and the binary function outputs.

Figure 1: An example activation function structure. The activation function is composed of multiple repetitions of the “core unit”, which consists of two inputs, two unary functions, and one binary function. Unary functions take in a single scalar input and return a single scalar output, such u(x) = x2 or u(x) = σ(x). Binary functions take in two scalar inputs and return a single scalar output, such as b(x1, x2) = x1 · x2 or b(x1, x2) = exp(−(x1 − x2)2).

This approach is just… *chefs kiss*. Walking the tightrope b/w having an automated search that looks through a wide array of options and still gets things done is a hard ask. This approach does that very well. I’m a fan of the utilization of “units”. People overlook the power of throwing in a few pre-engineered units into your search (just because you have an automated search doesn’t mean you can’t guide/bias it with some insight). Their utilization of controllers and units was one of the main motivations for writing this piece.

To ensure that the RNN only finds the most performant function, we use the validation accuracy as a reward.

Figure 2: The RNN controller used to search over large spaces. At each step, it predicts a single component of the activation function. The prediction is fed back as input to the next timestep in an autoregressive fashion. The controller keeps predicting until every component of the activation function has been chosen. The controller is trained with reinforcement learning

That is the gist of the search process. This setup is extremely impressive. You can steal their approach for your search/testing procedures. It’s similar to something we did when I was at Clientell, and it worked out really well.

Onto the next section. Let’s see what this search leads to.

Interesting Insights about Activation Functions

A huge plus with this automated search is that we can make more general claims about activation functions and their properties. The authors found 4 interesting trends-

1. Complicated activation functions consistently underperform simpler activation functions, potentially due to an increased difficulty in optimization. The best-performing activation functions can be represented by 1 or 2 core units.

2. A common structure shared by the top activation functions is the use of the raw preactivation x as input to the final binary function: b(x, g(x)). The ReLU function also follows this structure, where b(x1, x2) = max(x1, x2) and g(x) = 0.

3. The searches discovered activation functions that utilize periodic functions, such as sin and cos. The most common use of periodic functions is through addition or subtraction with the raw preactivation x (or a linearly scaled x). The use of periodic functions in activation functions has only been briefly explored in prior work (Parascandolo et al., 2016), so these discovered functions suggest a fruitful route for further research.

4. Functions that use division tend to perform poorly because the output explodes when the denominator is near 0. Division is successful only when functions in the denominator are either bounded away from 0, such as cosh(x), or approach 0 only when the numerator also approaches 0, producing an output of 1.

3 is pretty interesting to me because I’ve been looking into wavelets for data learning. I’m going to end this here as a teaser, but the periodicity seems powerful.

Things with large models often tend to be a bit wonky, since large models have more space to “memorize” the data. but these are still worth considering. The authors also tested the generalization of the top activation functions with bigger models, with promising results.

“To test the robustness of the top performing novel activation functions to different architectures, we run additional experiments using the preactivation ResNet-164 (RN) (He et al., 2016b), Wide ResNet 28–10 (WRN) (Zagoruyko & Komodakis, 2016), and DenseNet 100–12 (DN) (Huang et al., 2017) models. We implement the 3 models in TensorFlow and replace the ReLU function with each of the top novel activation functions discovered by the searches. We use the same hyperparameters described in each work, such as optimizing using SGD with momentum, and follow previous works by reporting the median of 5 different runs.”

The results are shown in Tables 1 and 2. Despite the changes in model architecture, six of the eight activation functions successfully generalize. Of these six activation functions, all match or outperform ReLU on ResNet-164. Furthermore, two of the discovered activation functions, x·σ(βx) and max(x, σ(x)), consistently match or outperform ReLU on all three models.

The most promising of these is the Swish activation function. Let’s take a look at that.

A look at the Swish activation function.

Swish is defined as x · σ(βx), where σ(z) = (1 + exp(−z))^(−1) is the sigmoid function and β is either a constant or a trainable parameter. The researchers chose Swish over the other “best” activation function because it generalized better.

Swish is the Camavinga of activation functions- it can take many forms. “If β = 1, Swish is equivalent to the Sigmoid-weighted Linear Unit (SiL) of Elfwing et al. (2017) that was proposed for reinforcement learning. If β = 0, Swish becomes the scaled linear function f(x) = x 2 . As β → ∞, the sigmoid component approaches a 0–1 function, so Swish becomes like the ReLU function. This suggests that Swish can be loosely viewed as a smooth function which nonlinearly interpolates between the linear function and the ReLU function. The degree of interpolation can be controlled by the model if β is set as a trainable parameter.”

Some of you non-mathematical people might be wondering why we care about the first derivative of Swish. The first derivative tells you how quickly your output grows/changes relative to the input. A large derivative means that you will have large changes for small changes in input (and vice-versa). Thus it is important to study the derivative of an activation function (some learning rate functions also use derivatives extensively). Analysis of the first derivative of Swish shows the following:

There are some more things I can cover but in my assessment, they aren’t super important. Let me know if you want me to cover any specific things that I’m leaving out. Now let’s get into the results of using Swish.

Results of Swish on Benchmarks

Section 5 of the paper starts with the following quote:

We benchmark Swish against ReLU and a number of recently proposed activation functions on challenging datasets and find that Swish matches or exceeds the baselines on nearly all tasks.

This is the first sentence. Very exciting but let’s get into the details to see if the improvements were substantial. The high-level overview of the performance is certainly strong, with strong performance across tasks. As you proceed, keep in mind that this paper is old, so new functions will hold up better. I picked this paper more for the mathematical insights and search process over the Swish function itself.

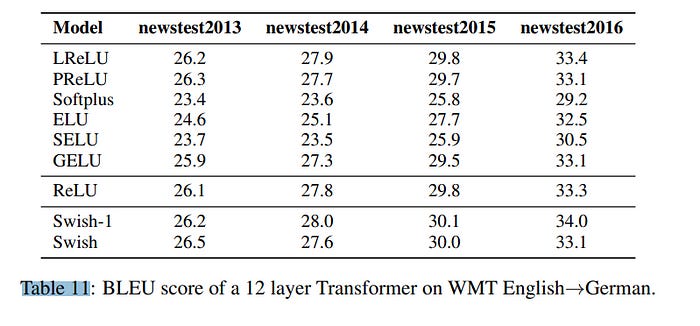
When comparing Swish to ReLU, on ImageNetSwish thoroughly outperforms ReLU.

Swish is competitive with the other more specialized functions. This is very impressive.

We see a similar performance on the CIFAR 10 and CIFAR 100 dataset. Therefore for computer vision, Swish seems to be far ahead of ReLU (and competitive with other more refined variants). What about Natural Language Processing (NLP) tasks? For that, the researchers use the standard WMT English →German dataset. The results here speak for themselves:

Closing

To me, Swish’s simplicity and ability to morph into other activation functions are compelling and warrant further exploration. Being an older publication, the results are outdated, but if I was writing this when it first came out: I would be spamming social media with 10,000 clickbait posts about the end of ReLU. A lot of clients I’ve consulted with still use ReLU w/o thinking (it’s almost 2024 y’all, be better), so updating that is low-hanging fruit to improve performance.

Most important to me is the approach taken here, the interesting mathematical insights, and the potential for future exploration. Looking into periodicity is promising, and we can always throw Evolutionary Algorithms to tackle search. The latter showed great promise in another Google Publication, “AutoML-Zero: Evolving Code that Learns”, where they used EAs to create ML algorithms. The results were impressive with Evolutionary methods even outperforming Reinforcement Learning.

The approach we propose, called AutoML-Zero, starts from empty programs and, using only basic mathematical operations as building blocks, applies evolutionary methods to automatically find the code for complete ML algorithms. Given small image classification problems, our method rediscovered fundamental ML techniques, such as 2-layer neural networks with backpropagation, linear regression and the like, which have been invented by researchers throughout the years. This result demonstrates the plausibility of automatically discovering more novel ML algorithms to address harder problems in the future.

The process may be visualized as below.

I’m mostly skeptical of AutoML (it’s extremely hard to do well and most startups that do AutoML are just burning investor money on a useless product), but this is one area where I see some potential.

If you liked this article and wish to share it, please refer to the following guidelines.

That is it for this piece. I appreciate your time. As always, if you’re interested in working with me or checking out my other work, my links will be at the end of this email/post. And if you found value in this write-up, I would appreciate you sharing it with more people. It is word-of-mouth referrals like yours that help me grow.

Reach out to me

Use the links below to check out my other content, learn more about tutoring, reach out to me about projects, or just to say hi.

Small Snippets about Tech, AI and Machine Learning over here

AI Newsletter- https://artificialintelligencemadesimple.substack.com/

My grandma’s favorite Tech Newsletter- https://codinginterviewsmadesimple.substack.com/

Check out my other articles on Medium. : https://rb.gy/zn1aiu

My YouTube: https://rb.gy/88iwdd

Reach out to me on LinkedIn. Let’s connect: https://rb.gy/m5ok2y

My Instagram: https://rb.gy/gmvuy9

My Twitter: https://twitter.com/Machine01776819