Google AI's Revolutionary Research on Quantum Chips [Breakdowns]

The secret to Google's recent Quantum Computing Chip, Willow, might be in DeepMind's Research on Machine Learning for Quantum Error Correction.

Hey, it’s Devansh 👋👋

In my series Breakdowns, I go through complicated literature on Machine Learning to extract the most valuable insights. Expect concise, jargon-free, but still useful analysis aimed at helping you understand the intricacies of Cutting-Edge AI Research and the applications of Deep Learning at the highest level.

I put a lot of effort into creating work that is informative, useful, and independent from undue influence. If you’d like to support my writing, please consider becoming a paid subscriber to this newsletter. Doing so helps me put more effort into writing/research, reach more people, and supports my crippling chocolate milk addiction. Help me democratize the most important ideas in AI Research and Engineering to over 100K readers weekly. Many companies have a learning budget that you can expense this newsletter to. You can use the following for an email template to request reimbursement for your subscription.

PS- We follow a “pay what you can” model, which allows you to support within your means, and support my mission of providing high-quality technical education to everyone for less than the price of a cup of coffee. Check out this post for more details and to find a plan that works for you.

---

Google’s Willow Chip has been attracting a lot of attention. By using Quantum Computing, the chip can do in 5 minutes what would take our most powerful supercomputer- 10²⁵ years to do (this is older than our universe). This had me interested in the mechanics of how this was accomplished.

My snooping eventually led me to DeepMind’s (Google’s AI Super-Lab) recent publication- “Learning high-accuracy error decoding for quantum processors”, which uses Machine Learning to detect and fix errors in Quantum Chips. Their approach-

• Outperforms every other technique.

• Scales to longer distances (we’ll talk about this).

• Has some interesting design decisions worth looking at.

Given some of the ideas and implications discussed, I’m fairly confident that this is a huge driver behind Willow’s success, and it will probably drive a lot of future advancements in the Quantum AI space. This makes AI-based Quantum Error Correction (especially leveraging Machine Learning) one of the most exciting emerging tech opportunities.

From a market perspective, I value it at a few hundred Million Dollar Opportunity in the short-medium term (within the next 2-5 years), which will creep up to the low billions within a decade to 15 years (for context, the entire Quantum Computing industry is estimated at 880 Million right now and estimated to grow to 100 Billion within this time frame. My bet is that as it matures, error correction becomes a proportionally smaller player in the market as more advanced capabilities are built). Given the utility of error correction, I also think it will have a much speedier time to revenue compared to a lot more “emerging” parts of quantum computing (even research groups would have to buy this tech).

However, the true value of such research is hard to estimate because it has the potential to rewrite our computation and rewire society. More details on the commercial and other major impacts of the market are given below (for the best experience, please look at the table below on a big screen)-

Economic Impact left empty b/c there are too many factors to account for before we can speak intelligently.

In the following Deep Dive, we will be looking at the paper to understand how the fiends at DeepMind were able to apply Machine Learning to QEC, making Quantum Computing more available-

Our decoder outperforms other state-of-the-art decoders on real-world data from Google’s Sycamore quantum processor for distance-3 and distance-5 surface codes. On distances up to 11, the decoder maintains its advantage on simulated data with realistic noise including cross-talk and leakage, utilizing soft readouts and leakage information. After training on approximate synthetic data, the decoder adapts to the more complex, but unknown, underlying error distribution by training on a limited budget of experimental samples. Our work illustrates the ability of machine learning to go beyond human-designed algorithms by learning from data directly, highlighting machine learning as a strong contender for decoding in quantum computers.

PS- I’ve picked up an interest in this field, so if you’re doing interesting things here, shoot me a message.

Executive Highlights (TL;DR of the article)

To understand this paper and its importance, we must first get some background in Quantum Computing and why QEC has been such a menace.

A two-liner on why QEC matters- A lot of people are very excited about Quantum Computing, and QEC is crucial to making Computing reliable enough for usage. “The global quantum computing market size was valued at USD 885.4 million in 2023 and is projected to grow from USD 1,160.1 million in 2024 to USD 12,620.7 million by 2032, exhibiting a CAGR of 34.8% during the forecast period”.

Source

The Problem: Why Quantum Error Correction Matters

Quantum computers are extremely sensitive to errors. Unlike classical bits that are either 0 or 1, quantum bits (qubits) exist in a superposition of states and are highly susceptible to:

• Environmental noise

• Control imperfections

• Interactions with other qubits

• Measurement errors

• Whatever other random bullshit error Life comes up with to make our modeling process that much harder.

These errors can cause decoherence — the loss of quantum information. For practical quantum computation, we need error rates around 10^-12 per operation, but current hardware has error rates of 10^-3 to 10^-2. This high rate of error would make the development of larger-scale computers (the kind that can be used as computers in the traditional sense) impossible since it will lead to errors in operations (image a bit getting flipped, causing you to send your bank transaction details publically).

These errors have been a huge reason why we’ve struggled to model Quantum Errors through traditional models accurately, as noted by the authors below-

If I ever become a rapper, “Leakage and Cross Talk” will be the name of my mixtape.

This is not a new problem and was first described by the legendary Richard Feynmann in the video below-

This is where QEC comes into play. Error Correction allows us to catch and fix those errors before running the computations, ensuring our transactions are executed safely. There are multiple ways to do this, but we will stick to discussing Surface Codes since that is what this research worked from.

2. Understanding Surface Codes for Quantum Error Correction

What is the Surface Code?

The surface code is a quantum error correction scheme that uses multiple physical qubits to encode one logical qubit (since each physical Qubit is very wimpy, we have them perform a DBZ style Fusion to form a Logical Qubit, which is more robust than an individual bit-

A qubit, unlike a normal bit which is 0 or 1, can be both 0 and 1 simultaneously due to a quantum phenomenon called “superposition”. This allows it to hold more information and explore multiple possibilities at once, leading to potential exponential speedups for certain computations. This reminds me a lot of our conversation around Complex Valued Neural Networks and how they seem to create richer representations since they model the data on the unit circle instead of a the number line (which is what Real Numbers do).

A Surface Code uses redundancy to protect information by doing some cool things:

• Creates a 2D grid of physical qubits

• Uses additional “stabilizer” qubits to detect errors

• This can detect errors without measuring (and thus destroying) the quantum state

• Has the highest known tolerance for errors among codes with planar connectivity- Compared to other quantum error correction codes where qubits are arranged on a 2D grid (planar), the surface code can withstand a higher rate of errors on its physical qubits before the encoded logical qubit’s information is corrupted. This “tolerance” is a crucial factor in determining the feasibility of building a fault-tolerant quantum computer.

There’s a lot of information, but for our purposes, it’s important to understand that it has the following key components-

• Data qubits: Store quantum information

• Stabilizer qubits: Used for error detection

• Parity checks: Measurements that detect errors without collapsing the quantum state (very important to keep the benefits of Quantum Computing).

• Code distance: The size of the grid (larger = more protection but more complex)

We will treat everything else as an implementation detail and move on for now. Just remember these 4 components and that all the homies stan Surface Codes.

“a, Data qubits (grey circles) on a d × d square lattice (here shown for code distance d = 5) are interspersed with X and Z stabilizer qubits (X and Z in circles). The logical observables XL (ZL) are defined as products of X (Z) operators along a row (column) of data qubits. b, In a memory experiment, a logical qubit is initialized, repeated stabilizer measurements are performed and then the logical qubit state is measured. During the experiment all qubits and operations are subject to errors (here symbolically shown as bit (X), phase (Z), and combined bit and phase flips (Y) acting on individual data qubits from time step to time step).”

Now is when things get fun (for us). Let’s get into the Machine Learning for Decoding Quantum Errors.

3. Machine Learning for Decoding

As you read the paper, you will constantly see the term Quantum Error Decoders. Decoders are essential components of quantum error correction. Their job is to analyze the error syndrome- the pattern of detected errors on the physical qubits. Based on this syndrome, the decoder infers the most likely errors that occurred and determines the appropriate correction to apply to the physical qubits to restore the correct logical state.

This is hard enough as is, but it becomes even harder when we remember that it must be performed quickly enough to keep up with the ongoing quantum computation, as uncorrected errors can accumulate and lead to computational failure (analogous to exploding gradients in AI)-

Source

The speed and accuracy of the decoder are, therefore, critical factors in the overall performance and reliability of a quantum computer.

So why has Machine Learning become such a powerful tool for this? Let’s discuss that next.

Why Use ML?

Traditional decoders like Minimum Weight Perfect Matching (MWPM) make assumptions about error patterns that don’t match reality. ML can:

• Learn complex error patterns directly from data. This is an idea we explored in depth in our guide to picking b/w traditional AI, ML, and Deep Learning. To summarize- when you have very complex systems modeling all the interactions is too unwieldy for humans, ML systems that extract rules from your data (fit a function to a data) can be your savior-

In this case, we don’t have all the rules, so we rely on ML.

• Adapt to specific hardware characteristics (and other variables) by using them as inputs.

• Handle noisy and incomplete information (iff done right). I actually got my start in Machine Learning applied to low-resource, high-noise environments, and very high-scale environments. You’d be shocked at how models can be extremely fragile and robust based on their training setup.

• Potentially achieve better accuracy

This is where we get AlphaQubit, “a recurrent-transformer-based neural-network architecture that learns to predict errors in the logical observable based on the syndrome inputs”. It is “designed to decode the surface code for a range of code distances and for experiments of arbitrary duration.”

4. Understanding AlphaQubit’s Approach

Let’s first decompose the recurrent transformer architecture into it’s two components:

1. Recurrent-

• Used to build state representation for each stabilizer

• Can process error syndromes over time

• Maintains a running state of error information

• Handles variable-length sequences

• Very cracked at error correction

2. Transformer-

• Self-attention captures relationships between different error locations

• Can learn complex spatial-temporal correlations

• Scales well with code distance

• Can incorporate both local and global error patterns

Other than that, the architecture features:

• Convolutional layers for local error patterns

• Soft readout processing for measurement uncertainty

• Two-stage training (pretraining + fine-tuning)

“a, One error-correction round in the surface code. The X and Z stabilizer information updates the decoder’s internal state, encoded by a vector for each stabilizer. The internal state is then modified by multiple layers of a syndrome transformer neural network containing attention and convolutions. The state at the end of an experiment is used to predict whether an error has occurred. b, Decoder training stages. Pretraining samples come either from a data-agnostic SI1000 noise model, or from an error model derived from experimental data using pij or XEB methods”

Another important architectural decision made in this paper is AlphaQubit's decision to go for circuit-level instead of qubit-level models. Qubit-level models simplify the problem by assuming errors occur instantaneously on individual qubits. Circuit-level models, conversely, consider errors arising during the execution of quantum gates, offering a more realistic representation of actual quantum hardware behavior. This stems from the fact that entanglement, crucial for creating redundancy in both models, also influences error propagation at the circuit level. When gates operate on entangled qubits, errors can spread, creating correlated errors that qubit-level models, assuming independent errors, fail to capture. Consequently, while more complex due to the need to account for temporal dynamics and entanglement-mediated error propagation, circuit-level models are essential for developing robust error correction strategies for real-world quantum computers.

“(a) 5 × 5 rotated surface code layout, with data qubits (dark grey dots), X and Z stabilizer qubits (labelled light grey dots, or highlighted in blue/red when they detect a parity violation) interspersed in a checkerboard pattern. Logical observables ZL and XL are shown as bold lines on the left and bottom grid edges respectively. (b) The recurrent network iterates over time updating a representation of the decoder state and incorporating the new stabilizers at each round. Three parallel lines indicate a representation per stabilizer. © Creation of an embedding vector Sni for each new stabilizer i = 1, …, d2 − 1 for a distance d surface code. (d) Each block of the recurrent network combines the decoder state and the stabilizers Sn = (Sn1, …, SnM) for one round (scaled down by a factor of 0.7). The decoder state is updated through three Syndrome Transformer layers. (e) Each Syndrome Transformer layer updates the stabilizer representations through multi-headed attention optionally modulated by an (optional) learned attention bias followed by a dense block and dilated 2D convolutions. (f) Logical errors are predicted from the final decoder state. The triple lines marked with * indicate a representation per data qubit.”

Our main article will focus on this.

This is obviously hard to pull off, but the researchers manage to do it-

5. Results and Implications

AlphaQubit achieved:

• Better performance than traditional decoders. In the image below, “Decoder performance is quantified by the logical error per round (LER), the fraction of experiments in which the decoder fails for each additional error-correction round4 (‘Logical error per round’ in Methods and Fig. 3a).” In the image below we see that AQ has the best scores (main graph) and the lowest LER- in the legend (tryhard).

“The 1 − 2 × logical error versus error-correction round for code distance-3 and distance-5 memory experiments in the Sycamore experimental dataset for the baseline tensor-network decoder (black), our decoder (red) and three variants of MWPM (shades of grey). The LER is calculated from the slope of the fitted lines. The error bars are the 95% confidence interval.”

• Handled realistic noise patterns

“LER of different decoders for Pauli+ noise at different code distances. For each code distance, our decoder (red) is finetuned on 100 million samples from this noise model after pretraining on a device-agnostic circuit depolarizing noise model (SI1000). MWPM-Corr (black) and PyMatching (grey) are calibrated with a DEM tuned specifically to the Pauli+ noise model with soft information. The error bars are bootstrap standard errors. a, Soft decoder inputs. Inset: detection event density of the Pauli+ simulation compared with the Sycamore experimental samples (error bars are standard error of the mean). b, Hard decoder inputs.”

• Scaled to larger code distances (look at b in the image above)

• Maintained performance over long computations

“The 1 − 2 × logical error after up to 100,000 error-correction rounds (a) and the corresponding LER (b) for PyMatching (grey), MWPM-Corr (black) and AlphaQubit (red) pretrained on SI1000 samples up to 25 rounds and finetuned on 108 distance-11 Pauli+ simulated experiments of 25 rounds. Both finetuning and test samples are Pauli+. We plot LER values only where the corresponding 1 − 2 × logical error value is above 0.1. The error bars are bootstrap standard errors.”

6. Future Considerations

Before you YOLO all your tendies into Quantum Computing, be cognizant of the following challenges remaining:

1. Speed optimization. The authors propose some techniques that can speed up decoders to make them more useful. This article will briefly touch upon them, but we have a whole series coming on training and inference optimization, so I won’t talk about it too much here.

2. Scaling to larger code distances

3. Integration with real quantum hardware

4. Handling logical operations beyond simple memory

That is my overview of this paper. The rest of this article will break down the Machine Learning behind Quantum Error Correction in a lot more detail, covering why the setup works and what can be done to improve it.

Before we proceed, my friend -Graham Locklear- is hiring student researchers in Inference Optimization. This role is ideal for a first or second-year Ph.D. student from a U.S. university. I’m attaching a brief part of the JD here. Reach out to him for more details-

If you’re looking for work, my guide on building Side Projects will be very helpful to you.

I put a lot of work into writing this newsletter. To do so, I rely on you for support. If a few more people choose to become paid subscribers, the Chocolate Milk Cult can continue to provide high-quality and accessible education and opportunities to anyone who needs it. If you think this mission is worth contributing to, please consider a premium subscription. You can do so for less than the cost of a Netflix Subscription (pay what you want here).

I provide various consulting and advisory services. If you‘d like to explore how we can work together, reach out to me through any of my socials over here or reply to this email.

How AlphaQuibit’s Architecture Leads to Superior Error Correction

Read through the following quote-

In this work, we present a neural-network architecture that learns to decode the surface code under realistic hardware-level noise. The network combines a number of problem-specific features. Its per-stabilizer decoder state representation — a vector for each of the d2 − 1 stabilizers — stores information about the syndrome history up to the current round. Convolutions allow the spatial dissemination of information between adjacent stabilizer representations and at longer range when dilated. Self-attention allows the stabilizer state vectors to be updated based on the current state of each of the other stabilizers giving full interconnection with a limited number of parameters. The pooling and readout network aggregate information from the representations of the relevant stabilizers to make a logical error prediction.

They throw a lot at us, so let’s take a deep breath, drink some water, and pick apart each sentence w/ Pirlo’s precision and elegance.

1. State Representation

Its per-stabilizer decoder state representation — a vector for each of the d² − 1 stabilizers — stores information about the syndrome history up to the current round.

The recurrently updated State representation is notable for several reasons-

Source

Vector Dimensionality Trade-off: The choice of per-stabilizer vectors, rather than a global state, enables parallel processing while maintaining locality. This is crucial because error propagation in quantum systems is primarily local but can have long-range effects.

Scaling Properties: The d² − 1 scaling is significant because:

• It matches the physical qubit layout exactly

• Scales quadratically scaling with system size (which can add to computational complexity)

• Maintains constant memory per stabilizer regardless of code distance

Historical Context: Previous approaches like MWPM treated errors as instantaneous events. The vector-based history allows the model to:

• Track error evolution patterns over time

• Learn temporal correlations in noise

• Identify recurring error patterns

This use of recurrence gets us some serious adaptability towards the future-

We demonstrate that AlphaQubit from the previous section, with its recurrent structure, can sustain its accuracy far beyond the 25 error-correction rounds that the decoder was trained on. We find its performance generalizes to experiments of at least 100,000 rounds

The next technique is a Hood classic.

2. Local Processing (Convolutions)

Convolutions allow the spatial dissemination of information between adjacent stabilizer representations and at longer range when dilated.

Key features:

• Standard convolutions for adjacent stabilizer interactions

• Dilated convolutions for longer-range patterns

• Multi-scale error pattern processing

Convolutions also take advantage of the max out the grid structure of Surface Codes since convolutions also typically rely on running a sliding window across your input to extract inputs-

Image Source

We have the Recurrence for temporal processing and the Convoutions for locality. So naturally, we need something for globalized spatial information. And luckily, we know a guy-

3. Global Processing (Self-Attention)

Self-attention allows the stabilizer state vectors to be updated based on the current state of each of the other stabilizers giving full interconnection with a limited number of parameters.

As we’ve mentioned several times, Self-Attention extracts quantitatively different features than Convolutions. Therefore, adding them in can throw in new kinds of wrinkles into your processing-

• All-to-all stabilizer interactions: Unlike convolutions, which only consider local neighborhoods, self-attention allows every stabilizer to interact with every other stabilizer in the grid. This enables the model to capture long-range dependencies and correlations that might be missed by local processing alone. This is crucial in scenarios where errors on one qubit can affect distant stabilizers, as can happen with cross-talk, entanglement, or error propagation chains-

“Each element in the sequence attends to (focuses on) other elements to understand their relationships. This enables Transformers to capture long-range dependencies more effectively than RNNs. Fluff words in the middle stop being as much of an issue, when your model looks at all the words at once.”

• Parameter-efficient global processing: While achieving all-to-all interactions, self-attention does so with a relatively small number of parameters compared to a fully connected network (the “giving full interconnection with a limited number of parameters”). This is more efficient than a fully connected network, which would scale quadratically with the number of stabilizers (and thus quartically with code distance). This efficiency is crucial for scaling to larger code distances, where the number of stabilizers grows rapidly.

• Dynamic attention weights for different error patterns: The attention mechanism assigns weights to the interactions between stabilizers, and these weights are dynamically adjusted based on the input error syndrome. This allows the model to focus on the most relevant stabilizer interactions for a given error pattern. For example, if a particular error syndrome suggests a localized error, the attention mechanism might assign higher weights to the interactions between stabilizers in the vicinity of the error while down-weighting interactions with distant stabilizers. This adaptability makes self-attention particularly effective at handling the diverse and complex error patterns that can occur in quantum systems.

In many ways, this seems like a spiritual successor to LSTMs. The long and short cells are replaced with the attention and convolutions, respectively, and we have a temporal aspect. Not sure where I’m going there, but LSTMs have also been using for denoising, which seems like a sister-problem to error correction. I could be very off here, but I think there might be good potential here (this paper mentions another time someone tried LSTMs, so I don’t think I’m the only one who sees something).

Some more details about the architecture.

Those are the major highlights of the architecture for me. I like how this design tailor-made each component to address a specific aspect of quantum error correction while working together as a cohesive system. It seems to work very well.

Time to end on a discussion of the training process for this bad-boy. Fortunately, this is fairly intuitive-

Understanding how AlphaQuibit was Trained

Because real experimental data are in limited supply, we train our decoder in a two-stage process (Fig. 2b). In a pretraining stage, we first prime the network based on samples from a generic noise model (such as circuit depolarizing noise, which describes errors in the device based on a Pauli error noise model) for which we can quickly generate as many samples as needed (for example, using a Clifford circuit simulator such as Stim43). In a finetuning stage, we optimize this model for a physical device by training on a limited quantity of experimental samples from the device.

In case you forgot, here is 2b-

Overall Structure: AlphaQubit uses a two-stage training strategy to address the scarcity of real-world quantum data:

1. Pretraining: Building a foundation using a generic noise model.

2. Fine-tuning: Specializing the model for a specific quantum device.

“With this two-stage training method, we achieve state-of-the-art decoding using current quantum hardware, and demonstrate the applicability of this decoder for larger-scale quantum devices.”

Pretraining Stage

In a pretraining stage, we first prime the network based on samples from a generic noise model (such as circuit depolarizing noise, which describes errors in the device based on a Pauli error noise model) for which we can quickly generate as many samples as needed

Input Data: Synthetic data generated from a generic noise model. The paper explores several options:

• Circuit Depolarizing Noise: A simplified model representing errors by Pauli gates. This model captures the general behavior of noise but doesn’t account for specific hardware characteristics.

• Detector Error Model (DEM): The paper says this- “A DEM43 can be thought of as an error hypergraph, where stochastic error mechanisms are hyperedges connecting the clusters of detectors they trigger. These mechanisms are independent and have an associated error probability. The DEMs we use were previously fitted4 to each experimental set using a generalization of the pij method”. I would break this down, but I have no idea what any of this means, and I don’t want to ChatGPT to give you an explanation that I don’t understand. I’m copying it here for the sake of completeness. If you understand these funny words, please help your boy out.

• Superconducting-Inspired Circuit Depolarizing Noise (SI1000): A device-agnostic model that approximates the noise characteristics of superconducting quantum computers. The model gives highest weight (5p) to measurement operations since they’re the noisiest in real superconducting quantum computers, while single qubit gates and idle time get much lower weights (p/10) as they’re more stable. This mimics how errors actually occur in physical quantum computers where different operations have very different error rates.

“SI1000 (superconducting-inspired 1,000-ns round duration) noise44 is a circuit depolarizing noise model comprising Pauli errors of non-uniform strengths, which approximate the relative noisiness of the various circuit processes in superconducting circuits: for example, as measurements remain a major source of errors in superconductors, measurement noise has weight 5p for noise parameter p. In contrast, single qubit gates and idling introduce only a small amount of noise, hence their relative strength is p/10.”

• This weighted approach helps the model learn realistic error patterns during pretraining by matching the actual error distributions seen in hardware, making the eventual fine-tuning on real device data more effective.

Purpose of Pretraining: To put things simply, Quantum Data is very very expensive. Using the cheaper (and much easier to produce) noise in this stage gives our AQ model the general feel for quantum noise so that it can easily move on to the next stage. This helps us somewhat make up for the lack of computing data available from quantum devices by giving our model exposure to the world-

Based on both, fine-tuning doesn’t seem to have a massive difference. Maybe in Quantum Computing, we need to squeeze out every last bit of performance, but the trend of fine-tuning not completely shaking up your architecture seems to be solid (unless I’m missing something here).

The authors also touch upon the power of pretraining here- “We note that even when pretraining with SI1000 samples, and without any finetuning, AlphaQubit achieves parity with MWPM-BP at code distance 5.”

Once we have our work set with the pre-training, we move on to the next stage, which refines the generalist performance for specific hardware-

Fine-tuning Stage

Input 1: Pretrained model states (the ‘knowledge’ of generic quantum errors)

Input 2: Limited experimental data from real quantum devices. This gives us real hardware noise patterns, allowing us to model device-specific error characteristics.

The fine-tuning adds the required expertise to be deployed on the device. Given that we want the model to specialize, the usual risks of fine-tuning are significantly mitigated, giving a viable strategy for future development.

All in all, this two-stage approach allows the model to achieve high accuracy with a limited amount of experimental data. It’s a form of transfer learning, where knowledge gained from a larger, more general dataset is applied to a smaller, more specific task. This is particularly important in quantum computing, where experimental data is expensive and time-consuming to acquire.

Before we leave, let’s briefly end by touching on some techniques that can help speed up the work. This will be fairly brief as an introduction to some ideas that will get dedicated deep dives soon. I wanted to mention it since this is one of the most important problems we need to solve-

Improve the Inference Speed of Quantum Decoders

There are several ways to accomplish the above-

“First, having established the accuracy that is achievable, optimizing the architecture and hyperparameters for inference speed is likely to deliver significant gains while maintaining that accuracy.”- Starting with better architecture and hyperparams will lead to quicker convergence reducing our costs. I’m particularly interested in CoshNet over here for several reasons-

• It’s also based on Complex Numbers, which should make it viable quantum computing.

• It doesn’t require any tuning.

• It can match performance from larger CNNs while being much smaller- making it a possible improvement to the Convolutions currently-

• And it is very robust, which would make it a good use-case for error detection.

“Fig 4 shows despite the considerable perturbations (blurring and Gaussian noise), CoShRem remain stable to most of the characteristic edges and ridges (two step discontinuity in close proximity).”

I’d love to see how it holds up here.

“Using faster components such as local, sparse or axial attention78, which restrict attention to a subset of stabilizer pairs, have the potential to deliver speed improvements.”- Sparse Attention is a pretty powerful technique (not super familiar with the other two). I’m particularly interested in the Diff Transformer (which I’ve been meaning to breakdown for a while now) given it’s inbuilt noise cancellation-

Transformer often over-attends to irrelevant context (i.e., attention noise). DIFF Transformer amplifies attention to answer spans and cancels noise, enhancing the capability of context modeling.

“Custom implementation to optimize for a particular hardware accelerator design and to remove memory access bottlenecks can also improve speed for a specific architecture.”- Pretty self explanatory.

Then we have knowledge distillation where, we “first train a large, accurate ‘teacher’ network on the task. Then we train a smaller ‘student’ network whose architecture is tuned for inference speed. In addition to the logical observable labels that were available to the teacher, the student network is trained to match the probabilistic outputs of the teacher. Optionally, the student can be trained to match the internal activations and attention maps of the teacher. These richer, denser targets have been shown to enable the student to achieve higher accuracy than could be achieved when training the student network without the teacher network. For increased accuracy, an ensemble of teachers can be distilled into a single student.”

By using the student for inference we keep our costs low.

“ lower-precision computation”,- Lower Precision Computation is the usage of lower precision numbers (imagine using 6.78 instead of 6.78966111). This can save a lot of memory and speed up computations when applied at a large scale (NNs can perform billions of computations). This is what quantization does.

“weight and activation pruning”- Essentially, not every weight is equal. Some determine your accuracy much more than others (the 80/20 principle). This can get very extreme. For example the researchers of Sparse Weight Activation Training dropped their training Flops 8x while keeping the performance loss to less than 5%.

“For ResNet-50 on ImageNet SWAT reduces total floating-point operations (FLOPS) during training by 80% resulting in a 3.3× training speedup when run on a simulated sparse learning accelerator representative of emerging platforms while incurring only 1.63% reduction in validation accuracy. Moreover, SWAT reduces memory footprint during the backward pass by 23% to 50% for activations and 50% to 90% for weights.”

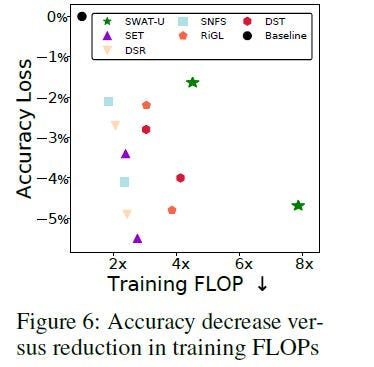
Another (even more radical) example of this is the MatMul Free LLMs, where the authors decided to full-send the efficiency by replacing all weights with -1,0, or 1. This led to 10x efficiency, while showing good performance and very promising scaling.

“Finally, custom hardware-specific implementation on application-specific integrated circuits or field-programmable gate arrays can deliver further speed improvements. Previous studies have demonstrated the feasibility of implementing decoders (for example, Union Find54 and neural network83) in such custom hardware. To best exploit application-specific integrated circuits and field-programmable gate arrays, low precision, fixed-point arithmetic and sparse networks may be necessary.”- Nerd hardware stuff that I will not dignify with further comments.

I’m going to end this article here. I know nothing about the Quantum side of Quantum AI, so there’s always a chance that I missed something/got it wrong. Please look into this (and other related research). DeepMind has made it open access, and it would be a shame to not take advantage of this opportunity.

More than anything, I hope this article helps you on your journey to Quantum AI. It’s an open field and a lot of land is there for the taking. Fields like QEC are also more accessible than other parts of quantum computing- so I think there is a lot of value to be captured by relatively smaller players.

Let me know what your thoughts are/what you think about this breakdown/research.

Thank you for reading and have a wonderful day.

Dev <3

If you liked this article and wish to share it, please refer to the following guidelines.

That is it for this piece. I appreciate your time. As always, if you’re interested in working with me or checking out my other work, my links will be at the end of this email/post. And if you found value in this write-up, I would appreciate you sharing it with more people. It is word-of-mouth referrals like yours that help me grow. You can share your testimonials over here.

Reach out to me

Use the links below to check out my other content, learn more about tutoring, reach out to me about projects, or just to say hi.

Small Snippets about Tech, AI and Machine Learning over here

AI Newsletter- https://artificialintelligencemadesimple.substack.com/

My grandma’s favorite Tech Newsletter- https://codinginterviewsmadesimple.substack.com/

My (imaginary) sister’s favorite MLOps Podcast-

Check out my other articles on Medium. : https://rb.gy/zn1aiu

My YouTube: https://rb.gy/88iwdd

Reach out to me on LinkedIn. Let’s connect: https://rb.gy/m5ok2y

My Instagram: https://rb.gy/gmvuy9

My Twitter: https://twitter.com/Machine01776819