Can AI be used to predict chaotic systems [Investigations]

Applications include the Three Body Problem, Financial Analysis, Climate Forecasting, Disaster Planning, Biomedical Engineering, Deepfake Detection, and Improving Language Models

Hey, it’s Devansh 👋👋

Some questions require a lot of nuance and research to answer (“Do LLMs understand Languages”, “How Do Batch Sizes Impact DL” etc.). In Investigations, I collate multiple research points to answer one over-arching question. The goal is to give you a great starting point for some of the most important questions in AI and Tech.

I put a lot of effort into creating work that is informative, useful, and independent from undue influence. If you’d like to support my writing, please consider becoming a paid subscriber to this newsletter. Doing so helps me put more effort into writing/research, reach more people, and supports my crippling chocolate milk addiction.

PS- We follow a “pay what you can” model, which allows you to support within your means. Check out this post for more details and to find a plan that works for you.

To see a World in a Grain of Sand
And a Heaven in a Wild Flower 
Hold Infinity in the palm of your hand 
And Eternity in an hour 

-Goes well with Fractals and their self-similarity.

Before we begin, we recently crossed 10 Million all-time reads across platforms. I wanted to do a special post, but wasn’t sure what would be most interesting. If you have any suggestions, please drop your recommendations.

Executive Highlights

I spent the weekend binge-watching the Three Body Problem series on Netflix (FYI- the books are probably the best sci-fi I’ve ever read, despite having horrible prose. The plot twists, characters, and themes are all elite). The main premise of an alien civilization in a world surrounded by three stars. This makes the planet’s weather very extreme and unpredictable, and the aliens decide to flee their star system and come to Earth b/c of its more stable climate. 

The series gets its name from the well-known Three-Body Problem in Math and Physics. The TBP is often used as one of the introductions to Chaotic Systems- systems where small changes to starting inputs can lead to dramatically different outputs (hence the well-known metaphor of a tornado formed by a butterfly flapping its wings). Given their high variance, chaotic systems are a menace to work with (for a good visualization of how things can change, check out the video below).

This got me thinking about how well AI can be applied to predict and manage chaotic systems. Chaotic Systems can be found in some of the world’s biggest challenges- such as climate change, financial markets, and our bodies. In this piece, I will be covering some interesting discoveries and parallels that I picked up from my research (not only was this field deeper than I expected, but writing about it also lets me write off my Netflix subscription as a “business expense”). The concepts we will cover have promising implications for disaster planning, climate forecasting, deep fake detections, and building the next generation of Language Models.

Optimal levels of chaos and fractality are distinctly associated with physiological health and function in natural systems. Chaos is a type of nonlinear dynamics that tends to exhibit seemingly random structures, whereas fractality is a measure of the extent of organization underlying such structures. Growing bodies of work are demonstrating both the importance of chaotic dynamics for proper function of natural systems, as well as the suitability of fractal mathematics for characterizing these systems. Here, we review how measures of fractality that quantify the dose of chaos may reflect the state of health across various biological systems, including: brain, skeletal muscle, eyes and vision, lungs, kidneys, tumours, cell regulation, wound repair, bone, vasculature, and the heart. We compare how reports of either too little or too much chaos and fractal complexity can be damaging to normal biological function... Overall, we promote the effectiveness of fractals in characterizing natural systems, and suggest moving towards using fractal frameworks as a basis for the research and development of better tools for the future of biomedical engineering.

-A Healthy Dose of Chaos: Using fractal frameworks for engineering higher-fidelity biomedical systems

Here are the main ideas I want to cover in this piece: 

1. Why Life is Chaotic: Many systems that we want to model in the world have chaotic tendencies. If I had to speculate, this is b/c a combination of three things leads to chaotic environments- adaptive agents, localized information, and multiple influences. Most large challenges contain all three of these properties, making them inherently chaotic.

2. Why Deep Learning can be great for studying Chaos: Deep Learning allows us to model underlying relationships in your data samples. Chaotic Systems are difficult to work b/c modeling their particular brand of chaos is basically impossible, and we must rely on approximations. DL (especially when guided by inputs from experts), can look at data at a much greater scale than we can, creating better approximations.

3. Fractals and Chaotic Systems: Fractals have infinite self-similarity. Thus, they can encode infinite detail in a finite amount of space. They also share strong mathematical overlap with chaotic systems- recursion, iteration, complex numbers, and sensitivity to initial conditions. This makes them powerful for modeling chaotic systems (that’s why they show up together in so much research). The reason I bring this up, is b/c it seems there are some bridges b/w NNs, Chaotic Systems, and Fractals. Studying these are great for future breakthroughs. 

4. Fractals and AI Emergence: An observation that I had while studying this: we can define chaotic systems from relatively simple rules. When studying emergent abilities in systems, this seems like an overlooked area to build upon. 

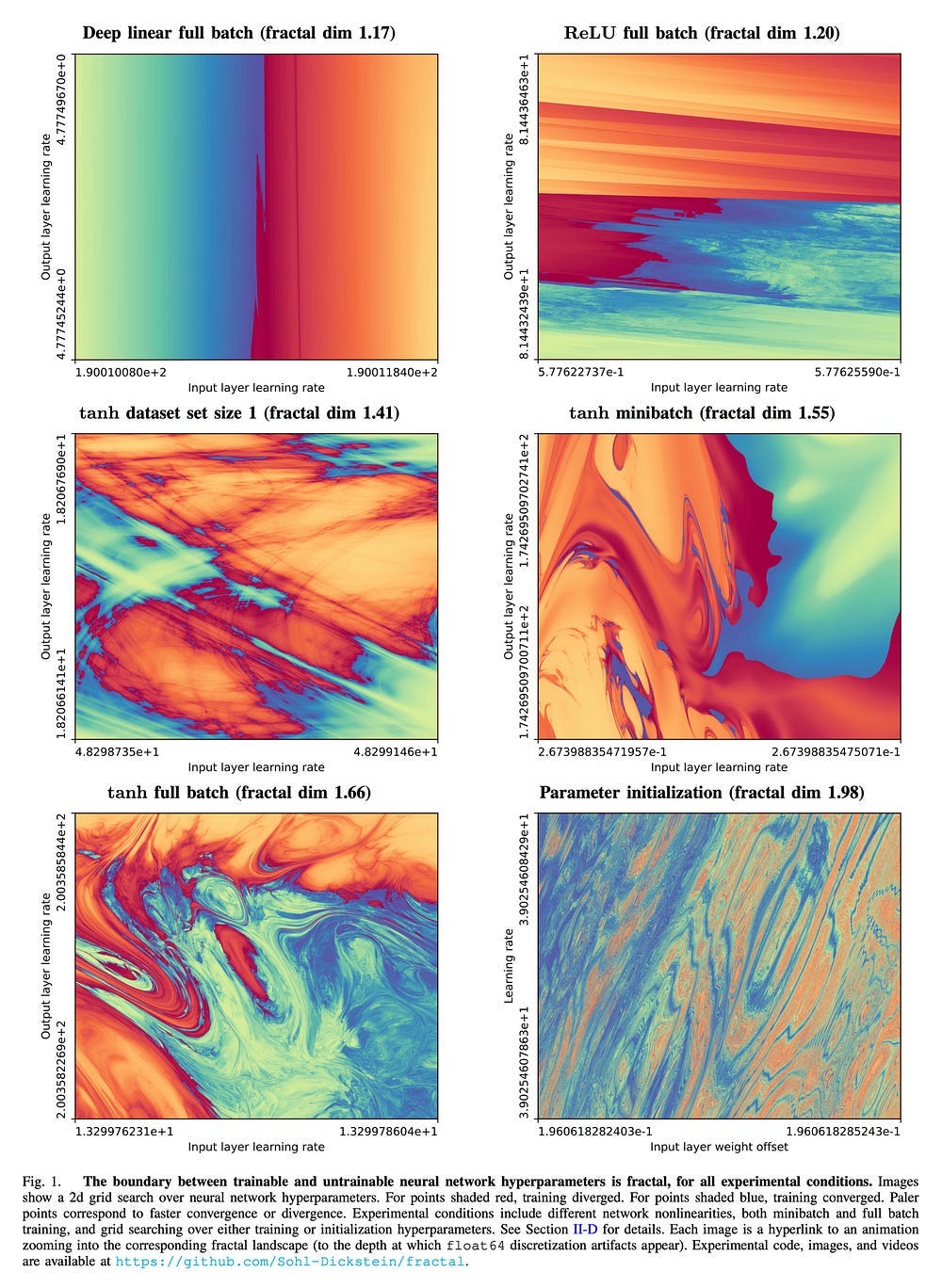
5. Fractals in Neural Networks: “The boundary between trainable and untrainable neural network hyperparameter configurations is *fractal*! And beautiful!”. Given the similarity in training NNs and generating Fractals, there is a lot of potential in utilizing Fractals to process patterns in data for one of the layers. Fractals might be great for dealing with more jagged decision boundaries (something that holds back NNs on Tabular Data), and would overlap very well with Complex Valued Neural Networks, which we covered here. 

We will elaborate on these ideas, touching upon different research on how various AI Tools are used to control/model chaos. There are too many important tangents so we will do separate follow-up investigations for each specific subdomain (for eg., we will do a separate, in-depth investigation for “AI and Chaos for Biomedical Engineering”). This article is meant more as an introduction to the overarching themes of utilizing AI for Chaotic Systems. 

We establish that language is: (1) self-similar, exhibiting complexities at all levels of granularity, with no particular characteristic context length, and (2) long-range dependent (LRD), with a Hurst parameter of approximately H=0.70. Based on these findings, we argue that short-term patterns/dependencies in language, such as in paragraphs, mirror the patterns/dependencies over larger scopes, like entire documents. This may shed some light on how next-token prediction can lead to a comprehension of the structure of text at multiple levels of granularity, from words and clauses to broader contexts and intents. We also demonstrate that fractal parameters improve upon perplexity-based bits-per-byte (BPB) in predicting downstream performance. 

-Fractal Patterns May Unravel the Intelligence in Next-Token Prediction

Why Life is Chaotic

To get you interested in this topic, my first order of business is to help you see why you should care about the intersection of AI and Chaos Theory. I could throw out a few use cases to show you how many important challenges this would apply to, but that is incredibly ugly. Nor would that provide you with underlying insight into why those use-cases are the way they are. Instead, let’s take the opposite approach. Let’s think about the nature of chaos, and what conditions lead to chaotic systems. 

The way I see it, 3 conditions lead to chaotic systems- 

1. Multiple Agents/Influences- No matter how interesting an individual agent or component might be, it will not be chaotic if it’s the only thing in a system. We need multiple agents or influencing factors that can interact with each other. 

2. Adaptable Agents- The agents in our system must be able to adapt to external circumstances, to change their behaviors (and hopefully even their objectives) with changes to their environments. 

3. Localized Information- Agents must only consider local information (they don’t know information about the entire system) as they make their decisions. This is the reason why Chess is Complex but not Chaotic (you can theoretically consider the entire world at any given time) while certain evolutionary algorithms exhibit chaotic behavior despite following somewhat simple rules.

Think about how many systems we work on that follow these properties. The cells in our body don’t have information about all the other cells/bacteria before acting on stimuli. Financial Market predictions utilize all manners of incomplete information. The world in itself can be modeled as a chaotic system. The next time you beat yourself up for being such a mess that can’t get their shit together, remember that it’s not you- it’s this world that’s chaotic. 

“Although the basis for fractal behaviour in natural systems is still unclear, its relationship to physiological state is much more pronounced. Variability has been analyzed with chaos and fractal theory in many different physiological systems, and the measure of fractality has been demonstrated to be associated with the state of health of the system”. This is absolutely insane.

This underlying chaos is why building good AI systems is so hard. Our data collection tends to apply a smoothening out effect, regularizing the jagged edges of individual data points to create smooth abstractions. This is great for models that make general statements about averages but falls apart when we start exposing these models to the absolute menace that is reality. Hence we get AI that works great on well-defined experiments and benchmarks but falls apart when we attempt to integrate it into broader, more dynamic solutions. 

There are remedies to this. Utilizing randomness has worked wonders for many use cases, b/c the randomness we inject acts as an approximation for the untamed wilderness of the world our AI system is about to enter. We’ve covered multiple instances of random data augmentation improving robustness and generalization in vision and NLP tasks, so figured I’d throw in something different here. Let’s look into how adding a kick of variance into weather models can improve performances 🌟🌟dramatically🌟🌟.

Weather forecasting is a very difficult challenge. Scientists have to slay a dual-headed hydra: if they use high-resolution grids (very small areas) for better accuracy, the computational overheads make the weather model impractical for scale; on the other hand, if they utilize lower res grids (with higher areas), the forecasts will fail when there is a lot of sub-grid variability in weather conditions. Turns out that doing some post-processing to account for the variation within the grid boxes leads to slay results. 

A low-cost post-processing technique improves weather forecasts around the world

 When it comes to modeling these chaotic systems, you will often see Deep Learning models play a very important role. Let’s cover why DL shines with chaotic systems. 

Deep Learning and Chaotic Systems

As we covered in our post, “How to Pick between Traditional AI, Supervised Machine Learning, and Deep Learning”: 

However, with very unstructured data, where identifying rules and relationships is very difficult (even impossible), Deep Learning can be the only way forward.

This fits Chaotic Systems to a t. They are challenging b/c we struggle to come up with adequately complex/nuanced models that can handle all variants of possible interactions. Deep Learning Models, which are really good at finding hidden rules and complex relationships, can significantly improve this process. Of course, we still need to adhere to good design, clearly demarcating the responsibilities of the components to reduce error and improve efficiency. Without doing the groundwork to set up your DL models, the best models will not save you. 

This was done very well in the paper “Combining Generative and Discriminative Models for Hybrid Inference”. In it, the authors look into various techniques to approximate trajectory estimation over three different datasets, “a linear dynamics dataset, a non-linear chaotic system (Lorenz attractor) and a real world positioning system”. They combined a Graphical Model with a Graph Neural Network, getting both the inductive bias of the former and the flexibility + scale of the latter.  

“Figure 2: Graphical illustration of our Hybrid algorithm. The GM-module (blue box) sends messages to the GNN-module (red box) which refines the estimation of x.”

This hybrid approach combining both “can estimate the trajectory of a noisy chaotic Lorenz Attractor much more accurately than either the learned or graphical inference run in isolation”. 

Figure 4: MSE with respect to the the number of training samples on the Lorenz Attractor.

The hybrid models here have good performance across the board for predicting paths. GNNs catch up with a high number of training samples, but performance across the board is better for the hybrid approach. For a more direct visual result, look below. Notice how the GNN has a few jittery paths, while the Hybrid Model is smooth across the board. 

Figure 1: Examples of inferred 5K length trajectories for the Lorenz attractor with ∆t = 0.01 trained on 50K length trajectory. The mean squared errors from left to right are (Observations: 0.2462, GNN: 0.0613, E-Kalman Smoother: 0.0372, Hybrid: 0.0169).

Another excellent demonstration of how to effectively combine Deep Learning with rule-based analysis for taming chaotic systems is demonstrated in, “Interpretable predictions of chaotic dynamical systems using dynamical system deep learning”. As the authors observe, “the current dynamical methods can only provide short-term precise predictions, while prevailing deep learning techniques with better performances always suffer from model complexity and interpretability. Here, we propose a new dynamic-based deep learning method, namely the dynamical system deep learning (DSDL), to achieve interpretable long-term precise predictions by the combination of nonlinear dynamics theory and deep learning methods. As validated by four chaotic dynamical systems with different complexities, the DSDL framework significantly outperforms other dynamical and deep learning methods. Furthermore, the DSDL also reduces the model complexity and realizes the model transparency to make it more interpretable.”

DSDL deserves a dedicated deep-dive (both b/c of how cool the idea is and b/c I don’t fully understand the implication of every design choice). While you wait, here is a sparknotes summary of the technique. 

1. What DSDL does: DSDL utilizes time series data to reconstruct the attractor. An attractor is just the set of states that your systems will converge towards, even across a wide set of initial conditions. The idea of attractors is crucial in chaotic systems since they are sensitive to starting inputs.

2. DSDL combines two pillars to reconstruct the original attractor (A): univariate and multivariate reconstructions. Each reconstruction has its benefits. The Univariate way captures the temporal information of the target variable. Meanwhile, the Multivariate way captures the spatial information among system variables. Let’s look at how. 

3. Univariate Reconstruction (D): This method reconstructs the attractor using the time-lagged coordinates of a single variable. Time-lagged coordinates are created by taking multiple samples of the variable at different points in time. This allows the model to capture the history of the system, which is important for predicting its future behavior. Imagine you are studying temperature fluctuations over time. The univariate approach would consider the temperature at a specific time, then the temperature at a slightly later time, and so on. This creates a sequence that incorporates the history of the temperature changes.

4. Multivariate Reconstruction(N): This method reconstructs the attractor using multiple variables from the system. This allows the model to capture the relationships between the different variables, which can be important for understanding the system’s dynamics. In the weather example, this approach might include not just temperature, but also pressure and humidity. By considering these variables together, the model can capture how they influence each other and contribute to the overall weather patterns. DSDL employs a nonlinear network to capture the nonlinear interactions among variables.

5. Finally, a diffeomorphism map is used to relate the reconstructed attractors to the original attractor. From what I understand, a diffeomorphism is a function between manifolds (which are a generalization of curves and surfaces to higher dimensions) that is continuously differentiable in both directions. In simpler terms, it’s a smooth and invertible map between two spaces. This helps us preserve the topology of the spaces. Since both N and D are equivalent (‘topologically conjugate’ in the paper), we know there is a mapping to link them. 

All of this allows DSDL to make predictions on the future states of the system. Here’s a simple visualization to see how the components links together-

Before we get into the results, I’d recommend that you take a look at this yourself for 2 reasons: 1- There is a lot I have to learn about Time Series Forecasting and (esp. about) dynamical systems; 2- I had to Google “diffeomorphism” for this. There’s a good chance that I’m missing some context or on some crucial detail. If you have any additions or amendments to my summary of this, I’d love to hear it. Your critique will only help me share better information (think of it as a contribution to open-sourcing the theoretical parts of AI Research). 

With that out of the way, let’s look at the numbers. DSDL clearly destroys the compeition- doubling or even almost tripling the performance of the next best across tasks.

Comparisons between the DSDL and other existing dynamical and machine learning methods in four different chaotic dynamical systems. Using the mean EPT (Lyapunov time), we compare the model predictive capabilities of different methods in four chaotic dynamical systems. The mean EPT is obtained by 100 different training/test sets, and the higher the mean EPT, the better the method performs.

There is also, “Learning skillful medium-range global weather forecasting” by the demons at DeepMind. I’m not going to get into it right now, but it works very well at predicting weather (including extreme events). Imagine how many lives this can save since it will enable better disaster planning. Another example of AI being used to handle chaotic systems (I promise we will do indepth explainations of both this specific paper and AI for weather forecasting). 

Here, we introduce GraphCast, a machine learning–based method trained directly from reanalysis data. It predicts hundreds of weather variables for the next 10 days at 0.25° resolution globally in under 1 minute. GraphCast significantly outperforms the most accurate operational deterministic systems on 90% of 1380 verification targets, and its forecasts support better severe event prediction, including tropical cyclone tracking, atmospheric rivers, and extreme temperatures. 

-Bar for bar, DeepMind dog walks every other major AI Research Lab. Google’s Product and Strategy teams need to get things sorted, b/c they are ruining a goldmine. 

To end this exploration, I figured I’d touch upon some interesting links that my research pulled up. It relates to Fractals, and how they seem to show up in unexpected places in Neural Networks. Furthermore, as we mentioned in the highlights, there seem to be overlaps between Neural Networks and Chaotic Systems. Given the possible bridges, I believe there are lots of possible breakthroughs to be made by exploring these intersections. 

Fractals, Neural Networks, and Chaos

Here are a collection of observations from my research for this article that I believe highlights interesting parallels between these fields- 

Fractals for Language Models

The aforementioned, “Fractal Patterns May Unravel the Intelligence in Next-Token Prediction” has some pretty interesting interesting takeaways for anyone interesting in NLP and LLMs. 

• Language has self-similar properties making it fractal-like.

• Different sub-domains of language have different structures. When it comes to fine-tuning, it might be working the structure of your underlying datasets to make sure they aren’t conflicting with each other- “the need in LLMs to balance between short- and long-term contexts is reflected in the self-similar structure of language, while long-range dependence is quantifiable using the Hurst parameter. For instance, the absence of LRD in DM-Mathematics is reflected in its Hurst parameter of H ≈ 0.5. Interestingly, the estimated median Hurst value of H = 0.70 ± 0.09 in language reflects an intriguing balance between predictability and noise that is similar to many other phenomena, and combining both H with BPB together yields a stronger predictor of downstream performance”

• Hurst Parameter can be used for better prediction of downstream ability. 

• Fractal Parameters are robust (I wonder if this is related to orthoganality that we will touch upon in later sections). 

Some of you may look at the paper and ask yourself, “What is the Hurst Parameter?” The Hurst Parameter (H) is a statistical measure that evaluates the long-term memory found within time series data. It shows how strongly the data trends, clusters, or reverts to a mean value over time.

The Hurst exponent falls between 0 and 1:

• H = 0.5: Indicates a random walk (no pattern or predictable direction).

• 0 < H < 0.5: Indicates an anti-persistent series (likely to revert to its long-term mean).

• 0.5 < H < 1: Indicates persistence (a trend is likely to continue in the same direction).

It has a pretty interesting relationship with Fractal Dimensions- 

Looking at the differing Hurst Values for the different domains might help in selecting better architectures and protocols for your tasks. And exploring the utilization for Fractals to embed language in an efficient way would be a big contribution (if it’s possible). 

Fractals and Hyper-params 

As shown in the best Twitter ever, “The boundary between trainable and untrainable neural network hyperparameter configurations is *fractal*! And beautiful!” 

“There are similarities between the way in which many fractals are generated, and the way in which we train neural networks. Both involve repeatedly applying a function to its own output. In both cases, that function has hyperparameters that control its behavior. In both cases the function iteration can produce outputs that either diverge to infinity or remain happily bounded depending on those hyperparameters. Fractals are often defined by the boundary between hyperparameters where function iteration diverges or remains bounded.”

Given how expensive training can be, I wonder if it would be possible to utilize Fractals to speed up training. 

Backprop in Training is Chaotic

Here is the abstract from, Backpropagation is Sensitive to Initial Conditions

“This paper explores the effect of initial weight selection on feed-forward networks learning simple functions with the backpropagation technique. We first demonstrate, through the use of Monte Carlo techniques, that the magnitude of the initial condition vector (in weight space) is a very significant parameter in convergence time variability. In order to further understand this result, additional deterministic experiments were performed. The results of these experiments demonstrate the extreme sensitivity of backpropagation to initial weight configuration.”

The last sentence is especially pertinent, given how much that makes Backprop sound like a chaotic process. Combine that with what we already asserted about Fractals showing up in Hyperparameter boundaries and I can’t be the only one who sees something special here. Studying chaotic systems might unlock some insights into Deep Learning (and vice-versa). 

Orthogonality, Complex Valued Neural Networks, and Fractals

The more I look into it, the more potential I see in Orthoganality and AI. We already looked into Complex Valued Neural Networks, which implement orthognality to great effect. 

The researchers behind, “Generalized BackPropagation, Étude De Cas: Orthogonality”, present “an extension of the backpropagation algorithm that enables us to have layers with constrained weights in a deep network.” They “demonstrate the benefits of having orthogonality in deep networks through a broad set of experiments, ranging from unsupervised feature learning to fine-grained image classification.” Their generalized BackProp algorithm seems to hold a lot of promise-

Figure 2: Convergence behavior of gBP and PGD for approximating eigenvectors of a matrix. gBP not only converges faster for this problem but also it achieves a lower loss

 Given the intersection between Reinmann Geometry and the Complex Plane, there should be a lot to explore over here. Furthermore, fractals link both Complex Valued Functions and chaotic systems. This sets up a nice three way relationship- 

1. Orthognality has been shown to improve performance of systems trying to model chaotic systems. 

2. Complex Valued Functions have demonstrated great potential in extracting robust features that are strong against perturbation. 

3. Fractals (or quasi-fractals) show up regularly in data. 

There is a natural synergy between these three, that is open for exploring. Computer Vision is probably the best suited for innovations combining these three fields given how all three rely on geometry (something that image data reflects very strongly). 

Every time I finish a piece like this, I am awed by the depth of human knowledge and by how much there is for me to learn. Hopefully, my work gets you interested in exploring these themes on your own. Nothing would be more gratifying. As I study the sub-domains of chaotic systems in more details, I will be sure to do follow-up investigations on each of those challenges and how AI can be used to solve them. If you have any insights you’d like to share, I’m always happy to talk about these ideas further. 

If you liked this article and wish to share it, please refer to the following guidelines.

That is it for this piece. I appreciate your time. As always, if you’re interested in working with me or checking out my other work, my links will be at the end of this email/post. And if you found value in this write-up, I would appreciate you sharing it with more people. It is word-of-mouth referrals like yours that help me grow.

Reach out to me

Use the links below to check out my other content, learn more about tutoring, reach out to me about projects, or just to say hi.

Small Snippets about Tech, AI and Machine Learning over here

AI Newsletter- https://artificialintelligencemadesimple.substack.com/

My grandma’s favorite Tech Newsletter- https://codinginterviewsmadesimple.substack.com/

Check out my other articles on Medium. : https://rb.gy/zn1aiu

My YouTube: https://rb.gy/88iwdd

Reach out to me on LinkedIn. Let’s connect: https://rb.gy/m5ok2y

My Instagram: https://rb.gy/gmvuy9

My Twitter: https://twitter.com/Machine01776819