Revolutionizing AI Embeddings with Geometry [Investigations]

How Angular Information can lift up LLMs and beyond

May 27, 2024

Hey, it’s Devansh 👋👋

Some questions require a lot of nuance and research to answer (“Do LLMs understand Languages”, “How Do Batch Sizes Impact DL” etc.). In Investigations, I collate multiple research points to answer one over-arching question. The goal is to give you a great starting point for some of the most important questions in AI and Tech.

I put a lot of effort into creating work that is informative, useful, and independent from undue influence. If you’d like to support my writing, please consider becoming a paid subscriber to this newsletter. Doing so helps me put more effort into writing/research, reach more people, and supports my crippling chocolate milk addiction.

Help me buy chocolate milk

PS- We follow a “pay what you can” model, which allows you to support within your means. Check out this post for more details and to find a plan that works for you.

Executive Highlights (tl;dr of the article)

A special thank you to Manny Ko, principal engineer at Apple for his constant sharing of great papers. This article is largely a synthesis of many interesting conversations and back-forths.

A lot of current research focuses on LLM architectures, data sources prompting, and alignment strategies. While these can lead to better performance, such developments have 3 inter-related critical flaws-

They mostly work by increasing the computational costs of training and/or inference.
They are a lot more fragile than people realize and don’t lead to the across-the-board improvements that a lot of Benchmark Bros pretend.
They are incredibly boring. A focus on getting published/getting a few pyrrhic victories on benchmarks means that these papers focus on making tweaks instead of trying something new, pushing boundaries, and trying to address the deeper issues underlying these processes.

This is what leads to the impression that “LLMs are hitting a wall”. However, there is a lot of deep research with game-changing implications. Today we will primarily be looking at 4 publications: “AnglE-optimized Text Embeddings”, “RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space”, “Angular Embedding: A Robust Quadratic Criterion”, and “Angular Embedding: A New Angular Robust Principal Component Analysis” to look at how we can improve embeddings by exploring a dimension that has been left untouched- their angles.

Angular Embeddings (AE) can dimensionality reduce the 4 classes better than other methods.

To understand what the main parts of this article, it’s important first to understand some background information

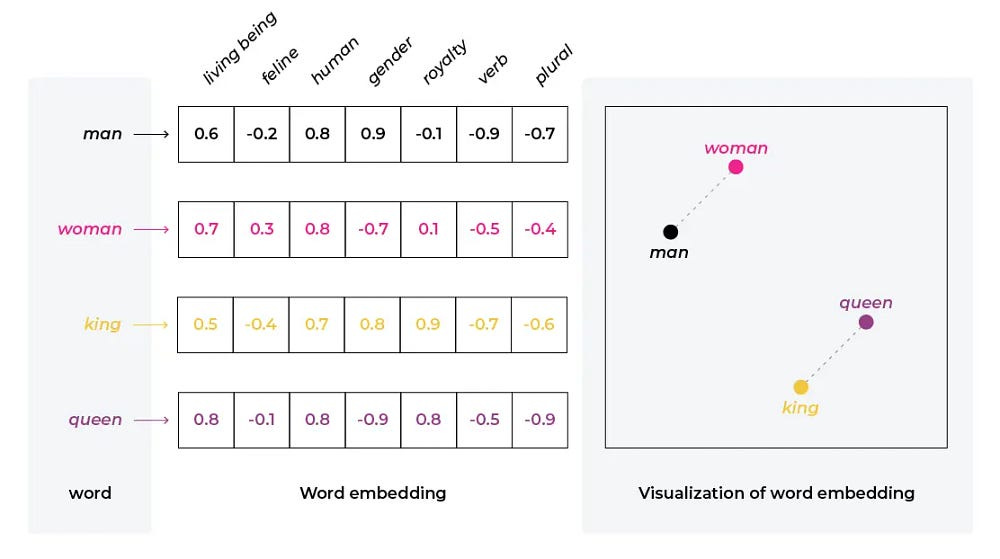
What are Embeddings? Embeddings represent complex data structures (words, sentences, knowledge graphs) as low-dimensional vectors in a multi-dimensional space. Ideally, you want similar concepts placed closer together, while dissimilar concepts are further apart.

Why Embeddings are Important in NLP? Good Embeddings allow three important improvements- Efficiency: By reducing operating on a lower dimensionality, we reduce the computational costs; Generalization: Embeddings enable models to handle unseen data by extending insights/structural similarity; Improved Performance: Lead to breakthroughs in various NLP tasks.
Challenges in Current Embeddings: Current Embeddings are held back by three things- Sensitivity to Outliers: Standard methods are highly susceptible to erroneous data; Limited Relation Modeling: Embeddings struggle to capture complex relationships in unstructured text; Inconsistency: Comparing similarity and dissimilarity changes based on specific data domains. Even within the same domain, we might have inconsistency in different sets of pairwise rankings, which messes up global rankings; and Computational Cost: Training sophisticated representations can be expensive.

Once you understand these challenges, we can explore the next generation of embeddings that utilize these pillars-

Complex Geometry: The complex plane provides a richer space to capture nuanced relationships and handle outliers. For text embeddings, this allows us to address a problem with Cosine Similarity called Saturation Zones- regions where the function’s gradient becomes very small, approaching zero. This can hinder the learning process in neural networks, especially during backpropagation.

The saturation zones of the cosine function. The gradient at saturation zones is close to zero. During backpropagation, if the gradient is very small, it could kill the gradient and make the network difficult to learn.

Focusing on angles rather than magnitudes avoids the saturation zones of the cosine function, enabling more effective learning and finer semantic distinctions.

(a) Division in complex space. ∆θ is the angle difference between dividend z and divisor w in complex space. (b) Angle optimization in cosine saturation zones. **Even though ∆y ≈ 0 could kill the gradient, the corresponding angle difference in complex space is still distinct for optimization.**

Those of you who were around when we covered natural gradients might see some strong parallels in the idea of using geometric information (that traditional techniques overlook) to reach better performance.

Orthogonality: means that the dimensions of the embedding space are independent of each other. This allows each dimension to represent a distinct feature or concept without being influenced by other dimensions. For example, if an embedding has dimensions for “color” and “shape,” a change in the “color” dimension should not affect the “shape” dimension. This independence helps the model to capture more nuanced relationships and avoid unintended correlations between features. In knowledge graphs, orthogonality can improve the ability to represent and infer complex relationships between entities and relations.

“In this paper, we present a new approach for knowledge graph embedding called RotatE, which is able to model and infer various relation patterns including: symmetry/antisymmetry, inversion, and composition. Specifically, the RotatE model defines each relation as a rotation from the source entity to the target entity in the complex vector space”

Contrastive Learning: Contrastive learning is a training technique that encourages similar examples to have similar embeddings and dissimilar examples to have distinct embeddings. The model learns by comparing examples and minimizing the distance between similar pairs while maximizing the distance between dissimilar pairs. Contrastive Learning has had some history with Text Embeddings, but negative samples in particular have been underutilized-

Blending these techniques together has a lot of potential. We have already covered the utility of Complex Networks in Computer Vision and Audio Processing. It’s not hard to see how all of these can be combined to build rich multi-modal embeddings.

We will spend the rest of this article getting into details on how we can use complex embeddings for both naked LLMs and Knowledge Graphs.

The procedures of the LLM-supervised learning. For the STS (semantic textual similarity) task, we use the prompt “You are a highly smart same-meaning/opposite-meaning sentence-generating system. Your job is to generate {size} synonymous/antonym sentences of a given input sentence. Input sentence: {text}. Output:” to generate positive/negative pairs. {size} and {text} are placeholders for the generated size and the input text, respectively.

I provide various consulting and advisory services. If you‘d like to explore how we can work together, reach out to me through any of my socials over here or reply to this email.

1. Improving Robustness and Richer Semantics through Embeddings in the Complex Space

A. Angular Embeddings (AE): Unlocking Robust Ordering

To summarize, what sets LS and AE apart is not their criteria but their representations. For both LS and AE, the variance and distance criteria lead to the same optima. AE represents the size and confidence of pairwise local orderings in single complex numbers and encodes the size and confidence of an optimal global ordering in the eigenvector of its transition matrix. As a quadratic criterion in the complex domain, AE has a nonconvex error function that is more sensitive to small errors yet at the same time more robust to large errors. The AE optimum can be viewed as the result of an iterative LS procedure where the confidence in local orderings gets adjusted according to the size of the embedding error.

The “Angular Embedding: A Robust Quadratic Criterion” proposes an interesting change to how we represent and handle ordering information. Instead of the traditional linear space, AE utilizes the complex domain, encoding pairwise comparisons as complex numbers within the unit circle.

LS and AE differ in the representation used for encoding the global ordering X (LS’s linear space versus AE’s angular space) and the objective function “ðXÞ used for measuring the quality of rank preservation (minimize the variance of neighbor estimates of the embedding for LS versus minimize the distance between the embedding and its neighborhood average for AE).

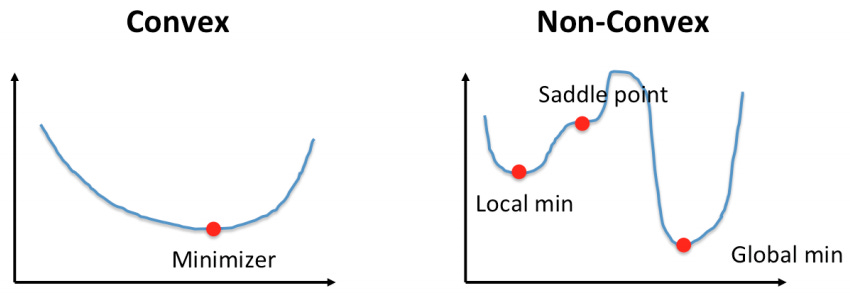
This approach captures not just the size of the difference between two elements (e.g., “A is 2 points better than B”) but also the confidence we have in that comparison (e.g., “We are 80% certain that A is better than B”). The angular representation also has profound consequences on the representations-AE’s error function is non-convex, meaning it has multiple local minima. This type of error function becomes more sensitive to small errors, allowing for fine-tuning of the embedding, but less sensitive to large outliers, preventing them from significantly affecting the overall solution.

Some of you may be wondering why that happens. Take convex functions like MSE (or LS here). When your error is small (<1) than squaring it, reduces the value (0.5 *0.5 =0.25). When error is large, squaring it increases the error (2*2=4). Non-convex functions like MAE (or AE) will flip this dynamic.

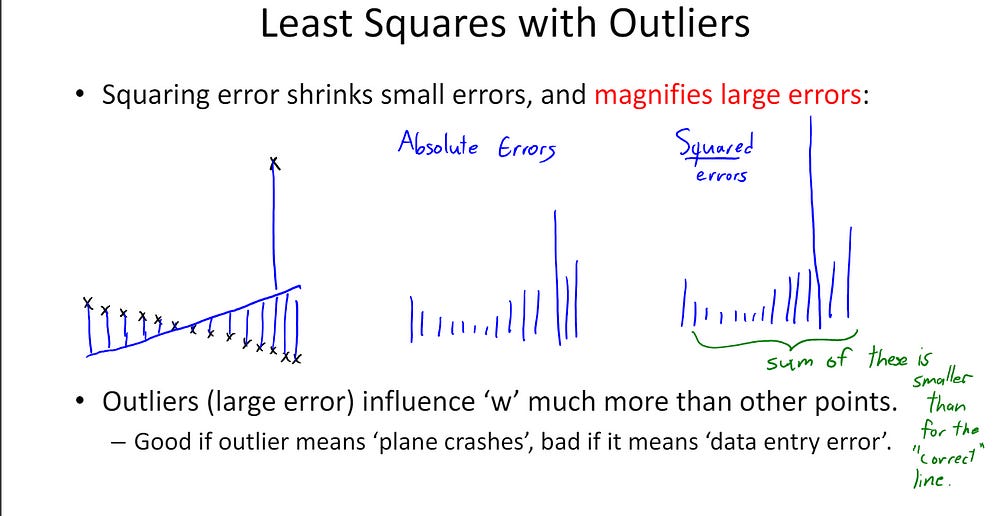
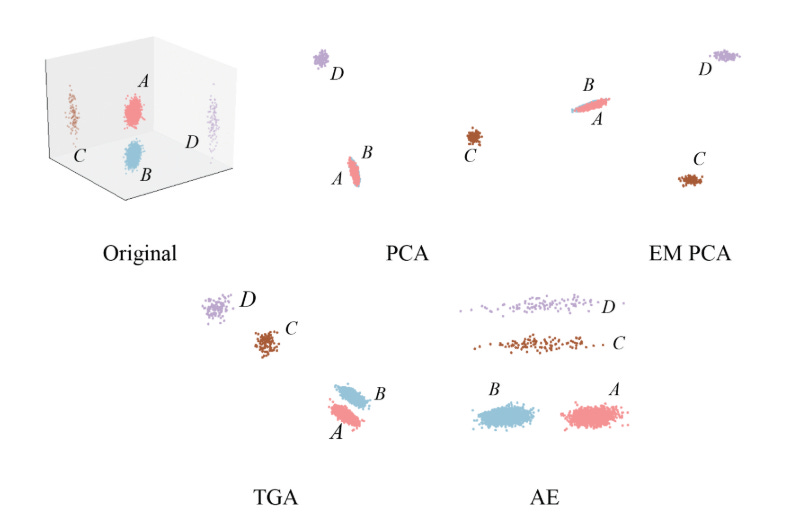
Don’t use things blindly. There is a depth to the the algorithms we use (even the basics). Study them. Source

We can see this in the image below. While both LS and AE can reconstruct the ground truth with no issues in normal conditions, AE absolutely sons LS when we add in more outliers.

**AE with a quadratic criterion in the complex domain is remarkably robust to outliers, unlike its real domain counterpart LS.** (a) A groundtruth surface with a height range of 1 and a maximal gradient magnitude of 0.16. (b) Gaussian noise with ¼ 0:05 is added to the pairwise height differences between pixels within a city-block distance of 2. Integration of these differences by LS and AE shows comparable reconstructions, both with a standard error of 0.0085. © Uniformly distributed outliers of values 3 are added to 10 percent of these noisy height differences. The standard error becomes 0.1666 for LS and 0.0184 for AE. **The surface reconstructed by LS is barely recognizable, while that by AE remains a close approximation to the ground-truth surface**

This, however, is far from the only way we can use complex numbers for embeddings.

B. RotatE: Modeling Relations as Rotations

“RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space” uses complex numbers for knowledge graph embedding. The authors models relations as rotations in complex vector space. We take triplet <h,r,t>(head, relation, tail), which models a relation r b/w h and t. RotatE’s key idea is that the tail entity embedding is obtained by rotating the head entity embedding according to the relation’s embedding.

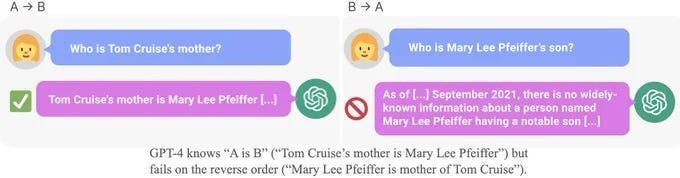
As you can see this approach allows us to both capture relationships between two entities at once (instead of having to define them individually). This might seem trivial, but I want to bring your attention to two important things. Firstly, this was written in 2019. Second, SOTA LLMs struggle with capturing relationships that are not structured in normal ways and will fail when the structure is very different to their pretraining (i.e. their generalization is worse than a League 2 players).

Large Language Models don’t understand Language

Since RotatE uses Geometry, it doesn’t have these issues. All we need to do is to define the relevant relationships with basic logic-

and then boop the entities on the complex plane. If the angles/relationships b/w them match our predefined rules (if statements), then we know they meet one our patterns-

RotatE: an example of modeling symmetric relations r with ri = −1

I feel like there’s a lesson here, but I can’t quite find it. Maybe my new Gen-AI powered chatbot can help me. I’ll publish the results in my NFT ebook covering synergistic AI algorithms, blockchain-enabled neural networks, and quantum-powered machine learning to optimize the metaverse for maximum disruption.

Now some of you may be wondering why we’re working with complex embeddings here. And that is exactly the kind of thinking you should do. After all, matching angles can be done with real numbers. So what advantage do complex numbers have? What would justify the overhead and additional complexity of the complex plane? Let’s talk about that next.

C. The Benefits of Complex Embeddings

The use of complex numbers for embeddings offers several key advantages:

Increased Representational Capacity: Complex numbers have two components (real and imaginary) compared to a single component for real numbers, enabling more expressiveness. Furthermore, complex analysis is built around the unit circle. This cyclical nature allows it to adapt very well to phasic data: images, signals, etc. This is very different to the real numbers, and is one of the biggest advantages of Complex Valued Neural Nets-

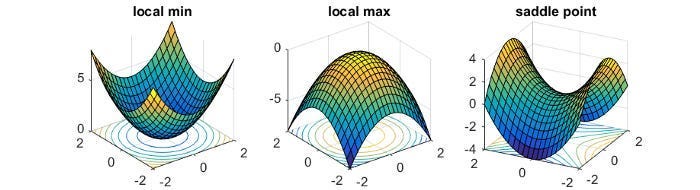
Complex Geometry- As the amazing CoshNet paper showed us, “The decision boundary of a CVnn consists of two hypersurfaces that intersect orthogonally (Fig. 7) and divides a decision region into four equal sections. Furthermore, the decision boundary of a 3-layer CVnn stays almost orthogonal [27]. This orthogonality improves generalization. As an example, several problems (e.g. Xor) that cannot be solved with a single real neuron, can be solved with a single complex-valued neuron using the orthogonal property”. Furthermore, They are critical points where the function attains neither a local maximum value nor a local minimum value.

Why does this matter? At saddle points, the derivatives of loss functions are still equal to 0. However, as the authors state, “SGD with random inits can largely avoid saddle points [29] [30], but not a local minimum.” This behavior is probably what allows for much faster convergence since the algorithms won’t get stuck in local minima. Overall, the unique geometry in the complex allow us to reach stable convergence quickly, without needing special hyper-parameter search and performance, which saves a lot of compute.

Robust Features: Using complex functions to process data allows us to capture more robust features, improving robustness in your pipeline.

Some of you are Arsenal fans and are thus incapable of getting the job done. You can drop out here. However, remember that the benefit of the complex plane comes from its unit-circle based geometry. This means that the true benefits of complex embeddings are unlocked by building ground up to reflect this. Let’s cover how next.

2. Beyond Distance: Optimizing Angles for Enhanced Semantic Discernment

A. Limitations of Cosine Similarity

While widely used in text embedding, the cosine similarity function has a critical limitation: saturation zones. When two embeddings are highly similar or dissimilar, the cosine function’s gradient becomes very small. This can lead to vanishing gradients during optimization, making it difficult to learn subtle semantic distinctions between text embeddings.

For supervised STS (Reimers & Gurevych, 2019; Su, 2022), most efforts to date employed the cosine function in their training objective to measure the pairwise semantic similarity. However, the cosine function has saturation zones, as shown in Figure 1. It can impede the optimization due to the gradient vanishing issue and hinder the ability to learn subtle distinctions between texts in backpropagation. Additionally, many STS datasets such as MRPC 1 and QQP 2 provide binary labels representing dissimilar (0) and similar (1), which naturally fall within the saturation zone of the cosine function.

Let’s talk about how to fix it.

B. Angle Optimization: AnglE’s Approach

The “AnglE-optimized Text Embeddings” paper addresses this challenge with AnglE, a text embedding model that focuses on optimizing angle differences in complex space. “It optimizes not only the cosine similarity between texts but also the angle to mitigate the negative impact of the saturation zones of the cosine function on the learning process. Specifically, it first divides the text embedding into real and imaginary parts in a complex space. Then, it follows the division rule in complex space to compute the angle difference between two text embeddings. After normalization, the angle difference becomes an objective to be optimized. It is intuitive to optimize the normalized angle difference, because if the normalized angle difference between two text embeddings is smaller, it means that the two text embeddings are closer to each other in the complex space, i.e., their similarity is larger.” This was demonstrated in the figure shown in the highlights-

The results end up resulting- “On the other hand, AnglE consistently outperforms SBERT, achieving an absolute gain of 5.52%. This can support the idea that angle-optimized text embedding can mitigate the negative impact of the cosine function, resulting in better performance.” AnglE ends up improving LLMs, “It is evident that AnglE-BERT and AnglE-LLaMA consistently outperform the baselines with a gain of 0.80% and 0.72% in average score, respectively, over the previous SOTA SimCSE-BERT and SimCSE-LLaMA.”

Table 2: Text embedding performance on STS tasks. We report the Spearman’s correlation ρ × 100 of the “all” setting computed by SentEval. For supervised LLaMA-based models, we fine- tuned them using the LoRA (Hu et al., 2021) technique and used the prompt “Summarize sentence {sentence} in one word:” sparked by (Jiang et al., 2023). Results marked with † are obtained from (Reimers & Gurevych, 2019), while results marked with ‡ are retrieved from (Gao et al., 2021). Additionally, results marked with ⋆ denote our own implementation using official code. For the remaining baselines, we refer to the corresponding original papers to obtain their results.

Very cool.

AnglE’s superiority in transfer and non-transfer settings, its ability to produce high-quality text embeddings, and its robustness and adaptability to different backbones

These are the two main components for building complex embeddings. The papers also leveraged contrastive learning + self-adversarial learning. We will cover these on later dates, in articles more focused on data generation and background setups. For now, I’m out. Have a great day.

If you liked this article and wish to share it, please refer to the following guidelines.

That is it for this piece. I appreciate your time. As always, if you’re interested in working with me or checking out my other work, my links will be at the end of this email/post. And if you found value in this write-up, I would appreciate you sharing it with more people. It is word-of-mouth referrals like yours that help me grow.